Как быстро складывать в уме: Как научиться быстро считать в уме любые числа: техники устного счета – Хотите быстро научиться считать в уме? 22 лучших способа!

Приёмы устного счета для быстрого вычисления в уме

Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.

Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?

Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!

Секреты устного счёта

Существуют приемы устного счета

— простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.

Прибавляем числа 7,8,9

Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.

Примеры:

56+7=56+10-3=63

47+8=47+10-2=55

73+9=73+10-1=82

Быстро складываем двузначные числа

Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».

Примеры:

54+39=54+40-1=93

26+38=26+40-2=64

Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.

Пример:

57+32=57+30+2=89

Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:

32+57=32+60-3=89

Складываем в уме трехзначные числа

Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.

Пример:

249+533=(200+500)+(40+30)+(9+3)=782

Особенности вычитания: приведение к круглым числам

Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.

Примеры:

67-9=67-10+1=58

576-88=576-100+12=488

Вычитаем в уме трехзначные числа

Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.

Пример:

843-596=843-500-90-6=343-90-6=253-6=247 

Умножить и разделить

Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!

Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:

15*16=15*10+(10*6+5*6)=150+60+30=240

Умножаем и делим на 4, 6, 8, 9

Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.

Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:

• умножить на 4 — это дважды умножить на 2;

• умножить на 6 — это значит умножить на 2, а потом на 3;

• умножить на 8 — это трижды умножить на 2;

• умножить на 9 — это дважды умножить на 3.

Например:

37*4=(37*2)*2=74*2=148;

412*6=(412*2)·3=824·3=2472

Аналогично:

• разделить на 4 — это дважды разделить на 2;

• разделить на 6 — это сначала разделить на 2, а потом на 3;

• разделить на 8 — это трижды разделить на 2;

• разделить на 9 — это дважды разделить на 3.

Например:

412:4=(412:2):2=206:2=103

312:6=(312:2):3=156:3=52

Как умножать и делить на 5

Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.

Пример:

326*5=(326*10):2=3260:2=1630

Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.

326:5=(326·2):10=652:10=65,2.

Умножение на 9

Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:

37*9=(37*3)*3=111*3=333

или

37*9=37*10 — 37=370-37=333

Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.

Счет на пальцах

Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.

Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:

• Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
• Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
• Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.

Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9.  А не проще ли, для умножения 5 на 9 выучить таблицу умножения?  Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.

Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь. 

Устный счёт на автомате

• Во-первых, необходимо хорошо знать состав числа и таблицу умножения.

• Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

• В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.

Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.

Эффективный счёт в уме или разминка для мозга / Habr

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»:

1800 + 200 + 190.
Еще пример:

31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899. 

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400;
3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68. 

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

600 : 25  = (600 : 100) x 4 = 6 x 4 = 24;
24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600. 

Теперь не кажется невозможным умножить в уме 625 на 53:

625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = 
= (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125. 

Возведение в квадрат двузначного числа

Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:

Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,

37^2 = 12 x 100 + 13^2 = 1200 + 169 = 1369; 
84^2 = 59 x 100 + 34^2 = 5900 + 9 x 100 + 16^2 = 6800 + 256 = 7056;

В общем случае (M — двузначное число):

Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:

195^2 = (100 + 95)^2 =  10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 70 x 100 + 45^2 = 10000 + (90+5) x 2 x 100 + 
+ 7000 + 20 x 100 + 5^2 = 17000 + 19000 + 2000 + 25 = 38025. 

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

M = 10m + n, K = 10a + 10 - n.

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001. 

У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,

48 x 42 = 2016.

99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,

99 x 91 = 9009.

Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:

95 x 95 = 9025. 

Тогда предыдущий пример можно вычислить немного проще:

195^2 = (100 + 95)^2 =  10000 + 2 x 100 x 95 + 95^2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 = 
= 10000 + 19000 + 1000 +  8000  + 25 = 38025. 

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Методика как научиться быстро считать в уме взрослому | SnatchNews

Многозначные числа.

Казалось бы, учиться считать, когда везде вокруг есть калькуляторы, гуглы и эксели, вообще не нужно. Но для себя всё равно прикольно. Хотя бы, чтобы чувствовать себя умным человеком, быстро считать сдачу в уме и не бояться Альцгеймера в старости. Прочитай и потом пройди тест, чтобы проверить, получается ли у тебя.

1. Как быстро складывать и вычитать простые числа?

   Легко вычесть из 16, например, 5, но мозг тормозит, когда надо перейти десятку. Например, чтобы из 16 вычесть 9, проще разбить 9-ку на 6 и 3 — сначала вычтем 6 (столько не хватает до 10) и потом 3. Получаем 7.

2. Как научиться быстро складывать многозначные числа?

   Складывай отдельно разряды. Например, если нужно сложить 456 и 732, то складывай сначала 400 и 700, потом 50 и 30, затем 6 и 2, а потом все три суммы вместе.

3. Как быстро вычитать многозначные числа?

   Тут мы разбиваем на разряды только вычитаемое число. Например, из 735 надо вычесть 259. Сначала вычитаем 200 (получаем 535), затем 50 (получаем 485), затем 9 — получается 476.

4. Как умножить многозначное число на однозначное?

   Здесь, как и при сложении, делим на разряды и умножаем отдельно каждый разряд на это число. Например, чтобы 345 умножить на 8, надо 300*8, 40*8 и 5*8 и посчитать сумму.

5. Как умножать между собой двузначные числа?

   Это уже тяжелее. Например, если 56 умножить на 38, то нам надо сначала 56*30, а потом 56*8 и сложить результаты.

6. Как быстро умножать на 11?

   Есть трюк — если умножаешь двузначноечисло на 11, то просто раздвигаешь это число и между 1 и 2 цифрой ставишь их сумму. Например, если 53*11 = 583. Если сумма больше 10, то добавляем единицу к первому числу. Например, 68*11 = 748.

7. Как узнать, делится ли число на 3?

   Если сумма чисел делится на три, то и само число тоже будет делиться на три. Например, число 522 не похоже на кратное трём, однако, если сложить 5+2+2 = 9, а 9 делится на 3. Значит и 522 делится на 3.

Как научиться быстро считать в уме

Умение быстро считать в уме – навык, который выделяет человека из толпы (особенно, когда нужно разделить счёт или проверить, не обсчитали ли вас при покупке глазированных сырков). Однако это именно навык, а не талант, которым обладают лишь избранные. Немного любопытства и регулярных тренировок – вуаля, вы научитесь так быстро проводить вычислительные операции в уме, что никто и не догадается, что вы гуманитарий! В этой статье расскажем, как научиться быстро считать в уме.

Как нужно тренироваться?

Во-первых, можно и выдумывать себе упражнения самостоятельно, но куда проще пользоваться приложениями из маркетов для смартфонов, выбор довольно широк. Также сначала стоит разобраться в азах счета — сложении, вычитании, делении и умножении. Все они имеют свои особенности, но разобраться в них нетрудно. Итак.

Сложение

• Сложение однозначных чисел.

Случаи, когда результат вычислений не превышает десяти, необходимо выучить, это основа. Если сумма превышает 10 — обращаемся к такому способу, как «опора на десяток». Смысл заключается в превращении первого число в 10, а из второго вычитании такого количества, которое нам понадобилось для этого превращения.

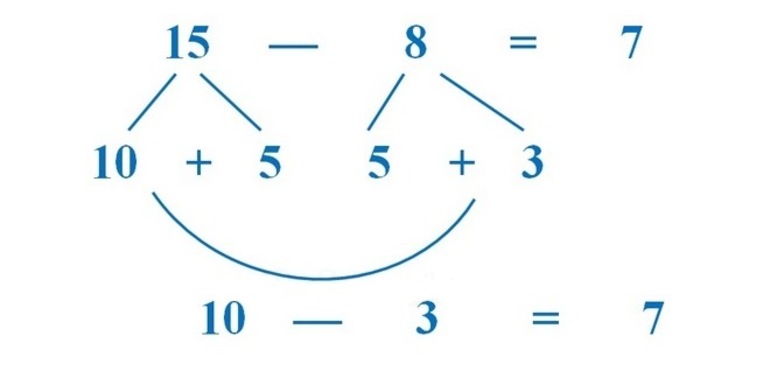
Например, складываем 7 и 8. Семёрке нужно добавить до десяти 3. Вычитаем эту тройку из второго числа, восьмерки (получим 5). И теперь прибавляем к 7, сколько нужно ей добавить до 10 (это 3), а после и остаток от 8 (это 5). Получаем 10 плюс 5, в итоге 15.

• Сложение многозначных чисел.

Данный принцип заключается в складывании схожих разрядов: тысяча с тысячей, сотня с сотней и т.п.

Например, есть 324 + 841. Разложим их: 324=300+20+4 и 841=800+40+1. Складываем схожие разряды из обоих слагаемых: 300+800=1100, 20+40=60, 4+1=5. Затем плюсуем числа, которые мы получили: 5+60=65, 65+1100=1165

Вычитание

• Вычитание однозначных чисел.

Однозначное минус однозначное проблем не должно вызывать. Если мы вычитаем однозначное из двузначного, лучше вспомнить об «опоре на десяток».

Например, есть  13 — 8. Чтобы из 13 получили десять, нужно вычесть 3. Вычитаем столько же из 8 и получаем 5. И вычитаем 10-5=5.

• Вычитание многозначных чисел.

Схоже со сложением, только быстрее и удобнее. На части раскладываем только вычитаемое.

Например, у нас есть 694 — 233. Раскладываем только 233 и получаем числа: 200, 30 и 3, и последовательно вычитаем их из 694. Так, 694-200=494, 494-30=464, 464-3=461. Получаем ответ: 461.

Умножение

• Умножение однозначного числа на двузначное или трехзначное.

По сути, мы при умножении поочередно складываем одно число указанное количество раз: 7 x 4=7+7+7+7.

Для умения быстрого умножения в уме нужно лишь вспомнить знакомую всем таблицу умножения.

Например, умножим 6 на 278.

Сначала уже привычно раскладываем многозначное: 278=200+70+8. Теперь умножаем их поочередно на 6: 200 x 6 =1200, 70 x 6 =420, 8 x 6 = 48.

И теперь складываем их по разрядам: 1200+420+48=1000+200+400+20+40+8=1000+600+40+20+8=1000+600+60+8=1668

• Умножение двузначных чисел.

На деле это оказывается не так сложно, как кажется. Как обычно, разберем на примере.

Итак, нам необходимо перемножить 26 и 49.

Разбиваем для упрощения 49 на 40 и 9. Тогда 26 x 40= 20 x 40 + 6 x 40= 800+240=1040.

И вторая часть: 26 x 9= 20 x 9 + 6 x 9= 180+54=134.

Складываем результаты, разложив по разрядам: 1040+134=1000+40+100+30+4=1000+100+70+4=1174

Деление

• Деление двузначного на однозначное.

Поделим 68 на 4.

Цель – найти множитель для четверки, чтобы получилось 68.

Подбором понимаем, что нужный нам множитель четырёх при котором в итоге в конце будет восьмерка — это 7,  4 x 7 = 28. Затем 68-28= 40.

Тогда 40 : 4= 10. В итоге получаем 48 : 3 = 17.

• Деление многозначного на однозначное.

Цель – взять самое большое «круглое» значение, что послужит нам делителем и не даст остаток.

Например, поделим 7395 : 3.

Выделим из многозначного наибольшую часть, чтобы поделить на 3 без остатка.

7395 недалеко от 7200 (3 x 24= 72, 7200= 72 x 100, получаем 2400). Осталось 7395-7200=395-200=300-200+95=195.

Также делим 195 на самый большой вариант цельного деления на 3, это будет 180. А 180:3=60.

После вычитаем 195-180=15. Вспоминаем, что 15= 3 x 5. Сложим все полученное: 2400+60+5=2465.

• Деление на двузначное

Здесь цель состоит в поиске границ, где будет искомое число.

Например, поделим 2520 на 35. Пробуем примерить, в каком из десятков прячется искомое.

Помним, что 3 x 7 = 21, попробуем умножить 35 x 70 = 2450.

Это ближайший десяток, ибо при прибавлении еще 350 получим 2800, а это больше нашего числа.

Получается, искомое число где-то посреди 70 и 80.

Тогда обратим внимание на крайние значения чисел в этом примере — 0 и 5.

На что необходимо умножить 5, чтобы получить в конце 0? Пробуем 2, 35 x 2 =70. Складываем  2450 и 70 и получаем 2520. Ответ:72.

Достаточно ли этого?

Этого достаточно для тренировок в уме. Однако главное правило заключается в регулярности и упоре на качество, а не на скорость. Старайтесь получать правильные ответы, а не быстрые, но хоть какие-нибудь. Постепенно все эти операции будут выполняться в вашей голове быстрее и быстрее, только не забывайте тренироваться. Теперь вы знаете, как научиться быстро считать в уме. Удачи!

Видео по теме

---

Подпишитесь на наши интересные статьи в соцетях!

Или подпишитесь на рассылку

---

Сохрани статью себе в соцсеть!

Вам будет также интересно:

Как научиться быстро считать в уме ℹ️ техника быстрого счета любых чисел в уме, приемы и способы для взрослых и детей, правила и примеры

Нюансы, которые следует учитывать

Чтобы научиться умножать двузначные числа или складывать дроби, придется потратить достаточно много времени. Однако для более быстрого обучения важно концентрировать внимание на трех основных моментах, без которых время будет потрачено впустую:

1. Концентрация внимания. Процесс обучения будет куда более эффективным, если математик научится фокусировать свое внимание на той задаче, которую выполняет, ведь очень часто приходится отвлекаться на различные внешние факторы, которые не позволяют быстро посчитать или сложить в уме сложные числа. Чтобы такого не происходило, важно научиться концентрироваться на выполнении лишь одной задачи за один раз. Для этого стоит найти для место, где никто не будет мешать, а также постараться отбросить все мысли о работе, личной жизни, планах на будущее и прочем.
2. Формулы. Чтобы производить вычисление даже сложных математических уравнений в уме, придется запомнить основные формулы и теоремы, по которым это можно сделать. Само собой, чтобы найти неизвестную переменную, иногда можно использовать и банальный метод подбора, однако такой способ является гораздо более сложным. Поэтому важно выучить всю теоретическую информацию, которую можно будет использовать: формулу дискриминанта, теорему Виета и прочие математические хитрости, с помощью которых процесс счета упрощается в несколько раз.
3. Практика. Как бы это парадоксально ни звучало, но чтобы освоить технику быстрого счета в уме, необходимо для начала научиться выполнять те же задачи на листке бумаги. Ведь записывая выполнение того или иного упражнения, можно всегда посмотреть, где именно была совершена ошибка в процессе тренировки и сделать кое-какие выводы. Как только арифметик научится легко решать сложные примеры в тетради, самое время переходить на устный счет.

Как только все правила и теоремы будут запомнены, а человек научится не только решать сложные задачи на листке бумаги, но и концентрировать свое внимание, можно приступать к процессу обучения устному счету. Под каждое математическое действие существует свой особый прием и даже несколько тренажеров, позволяющих освоить технику гораздо быстрее.

Вот и польза от интернета

Чтобы научить ребенка считать в уме, можно скачать ему на телефон специальное приложение, в котором есть огромное количество различных примеров, на решение которых дается от 2 до 5 секунд. Само собой, можно попытаться составить уравнения и задачи самому, однако практика показывает, что в большинстве случаев они получаются крайне однообразными и не несут большой пользы. Также существуют специальные сайты, которые позволяют своим посетителям решать уравнение и сложные задачки в режиме онлайн. Используя такие платформы, самое главное — подобрать под себя правильный уровень сложности.

Чтобы система обучения приносила как можно большую пользу, важно понять, что вовсе не обязательно часами сидеть за примерами или пытаться решить сложные задачи сразу в уме. Ментальный счет — это долгий и кропотливый процесс, который не терпит спешки, и чтобы учиться правильно, достаточно уделять примерам от 5 до 10 минут в день. В противном случае голова будет напрягаться, а ученик начнет совершать глупейшие ошибки. Со временем даже такое «микрообучение» приведет к потрясающим результатам. Нужно лишь набраться терпения и практиковаться согласно рекомендациям математиков.

Сложение двузначных и трехзначных чисел

Как в первом классе детей учили быстро складывать и вычитать в уме однозначные числа? Правильно, позволяли для этого использовать пальцы. Ну а умножение и деление были освоены благодаря специальной таблице. Однако большинство взрослых, решивших научиться быстро считать в уме любые числа, как правило, умеют проводить эти действия не только с однозначными, но и с двузначными числами. В этом случае практиковаться будет значительно легче.

Однако если подросток не может сложить два двузначных числа, то сначала придется освоить именно эту методику, ведь от нее все и отталкивается. Как это сделать? Достаточно просто разбить двузначное число на десятки и единицы. То есть если перед учеником стоит пример 65+18, то необходимо каждое число сначала разложить: 65=60+5, 18=10+8. После этого складываем в уме десятки, а уже потом единицы: 60+10=70, 5+18=13. Если в процессе получается еще одно двузначное число, которое будет всегда состоять из одного десятка, то достаточно лишь прибавить сначала его, а уже потом — все имеющиеся единицы: 70+10=80, 80+3=83. Все довольно просто.

Однако когда речь заходит о трехзначных числах, то большинство людей почему-то сразу же входят в ступор, хотя методика здесь практически ничем не отличается от той, которая уже известна. Для начала необходимо разбить основное число на сотни, десятки и единицы, после чего начать складывать их между собой. Вот небольшой пример: 528+376. Действовать нужно по тому же алгоритму, что и ранее:

• Разбить числа: 528=500+20+8, 376=300+70+6.
• Сложить сотни: 500+300=800.
• Сложить десятки: 20+70=90.
• Сложить единицы 6+8=14.
• Сплюсовать все, что есть: 800+90+10+4=800+100+4=900+4=904.

Иногда, складывая десятки, также может получаться число больше сотни. Пугаться в этом случае не стоит. Достаточно будет просто прибавить одну сотню к уже имеющимся, после чего проводить арифметические действия с оставшимися десятками. Самое главное — не ошибиться в процессе.

Особенности вычитания

В математике существует всего два «полноправных» действия — сложение и умножение. Вычитание и деление являются обратными от этих двух. Кроме того, их всегда можно заменить умножением, подставив число «x», или сложением, подставив знак минус к неизвестному слагаемому. Именно поэтому, чтобы научиться вычитанию, сперва необходимо научиться складывать числа. Ведь в любой момент можно просто поменять в уме переменные и проверить правильность решения с помощью «x». Методика вычитания трехзначных чисел практически ничем не отличается от сложения. Вот небольшой пример: 553−192, а также подробный разбор:

• Разбить имеющиеся числа на сотни, десятки и единицы: 500=500+50+3, 192=100+90+2.
• Провести вычитание с сотнями: 500−100=400.
• Вычесть десятки, заняв одну сотню: 150−90=60.
• Вычесть единицы: 3−2=1.
• Сложить остатки, не забыв о заемных сотнях или десятках: «300+60+1=361».

То есть даже в вычитании будет обязательно присутствовать сложение. Основная сложность расчета таких примеров заключается в постоянной необходимости занимать десятки. Однако если проводить такую тренировку ежедневно, то со временем считать трехзначные числа будет ненамного сложнее, чем двухзначные. Самое главное — верить в себя и собственные силы.

Секреты умножения

Вот человеку нужно посчитать, находясь возле кассы, сколько же будет стоить 4 килограмма клубники по 183 рубля. Для этого он вытаскивает из кармана телефон и долго ищет в меню калькулятор. Однако куда быстрее будет посчитать все в уме. Самое главное — знать методику, которая позволяет это делать максимально правильно, а также как можно больше практиковаться. Алгоритм действий выглядит следующим образом.

• Разложить основное число, как и в случае с умножением: 183=100+80+3.
• Умножить число 4 на каждое имеющееся слагаемое: 100*4=400, 80*4=8*4*10=32*10=320, 3*4=12.
• Сложить все имеющиеся числа: 400+320+12=700+32=732.

Ничего сложного в этом нет, не говоря уже о том, что в умножении существует довольно много приемов, позволяющих провести операцию гораздо быстрее. К примеру, если человеку необходимо умножить какое-то число на 25, то достаточно просто разделить его на 4, после чего умножить на 100. Вот небольшой пример: 400*25=400/4*100=100*100=10000. Почему именно 4 и 100? Просто число 25 было замещено десятичной дробью ¼, ведь 25 — это 1 часть из 4 у сотни. Так что подобным приемом можно пользоваться, если необходимо быстро умножить что-то на «четвертак».

Сложности деления

Деление — самое сложное арифметическое действие, которое крайне трудно совершать в уме. Однако существует одна методика, которая является практически беспроигрышной. Как уже говорилось ранее, деление не является самостоятельным действием, поскольку оно обратное от умножения. Ведь что такое 32:8? Правильно: «x*8=32». Ну а по таблице умножения всем хорошо известно, что вместо переменной необходимо поставить число 4. Таким приемом можно пользоваться и для того, чтобы научиться быстро считать в уме.

Взрослому человеку это не составит большого труда, а вот ребенку придется сперва познакомиться с тем, что такое неизвестные переменные и как их искать.

Если человек научился проводить умножение с трехзначными числами в уме, то ему не составит особого труда для того, чтобы разделить эти числа. Вот небольшой пример: 795:3. Казалось бы, что посчитать его крайне трудно, но, чтобы упростить задачу, можно разбить его на множители, а также ввести переменные:

• Разбить число 795 на слагаемые, с которыми легко провести деление: «795=600+195».
• Поделить число 600 на 3 и держим в уме ответ: 200.
• Разделить число 195 на 3, но здесь необходимо также разделить его на слагаемые: 195=150+45.
• Поделить крупное число на 3: 150:3=50 и прибавляем ответ к имеющемуся: 200+50=250.
• Не зная таблицы деления, ввести переменную «x» для оставшегося числа 45=x*3. Получается, что x=15.
• Сложить остатки и проверить ответ умножением: 250+15=265, 265*3=200*3+60*3+5*3=795″ — все сходится.

Таким образом, чтобы облегчить процесс деления, можно воспользоваться не только методом разложения числа на слагаемые, но и вводя новую переменную. Особенно полезным этот навык окажется для того, кто проводит математические действия с более интересным и сложными примерами. Несколько месяцев практики обязательно принесут плоды, но следует взять себе за привычку проверять решение не с помощью калькулятора, а умножения.

Высчитывание процентов

Многие люди впадают в ступор, когда их просят найди 6 процентов от 253. Однако если знать основные математические правила, то в этом нет абсолютно ничего сложного. Причем, чтобы научиться проводить все действия в уме, не потребуется нескольких лет практики. Достаточно лишь следовать определенному алгоритму действий:

• Найти 1% от имеющегося числа. Для этого его необходимо разделить на 100: «253:100=2,53».
• Разложить получившиеся число на слагаемые, которые будет легко умножить на 6: 2,53=2+0,5+0,03.
• Провести умножение: 2*6=12, 0,5*6=½*6=3, 0,03*6=0,18.
• Сложить получившиеся значения: 12+3+0,18=15+0,18=15,18.

Чтобы научиться считать числа в уме, вовсе не обязательно быть вундеркиндом или потратить годы практики. Достаточно просто знать основные правила и формулы, которые позволяют упростить те или иные действия, а также уметь грамотно заменить некоторые переменные. Ну и, пожалуй, важнее всего — концентрироваться на выполнении определенной задачи. Если решать такие примеры каждый день, то со временем от калькулятора можно будет отказаться вовсе, что очень удобно, ведь даже в век информационных технологий полностью положиться на машины нельзя.

как научиться считать в уме

«Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят вам научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».

Тренировка устного счета

Есть люди, которые умеют совершать несложные арифметические операции в уме. Умножить двузначное число на однозначное, умножать в пределах 20, перемножить два небольших двузначных числа и т.д. – все эти действия они могут производить в уме и достаточно быстро, быстрее среднего человека. Часто этот навык оправдан необходимостью постоянного практического использования. Как правило, люди, которые хорошо считают в уме, имеют математическое образование или, по крайней мере, опыт решения многочисленных арифметических задач.

Несомненно, опыт и тренировка играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые, в отличие от вышеописанных, способны считать в уме гораздо более сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать сложные арифметические операции, которые не каждый человек и в столбик сможет посчитать.

Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме. Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета.

Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете «переплюнуть» даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Уроки на сайте

Уроки устного счета, представленные на сайте, направлены именно на развитие этих трех составляющих. В первом уроке рассказано, как развить в себе предрасположенность к математике и арифметике, а также описаны основы счета и логики. Затем дан ряд уроков по специальным алгоритмам для совершения различных арифметических операций в уме. И наконец, в данном тренинге представлены дополнительные материалы, помогающие тренировать и развивать умение считать устно, для того, чтобы суметь применить свой талант и свои знания в жизни.

Урок 1. Способности. Упражнения и рекомендации по развитию устного счета, внимания, краткосрочной памяти.

• Урок 1. Внимание и концентрация при счете в уме

Уроки 2-7. Алгоритмы. Что касается методик, то они даны в следующих уроках, которые разделены на несколько видов:

• Урок 2. Простые арифметические закономерности
• Урок 3. Традиционные методы умножения двузначных чисел
• Урок 4. Частные методики умножения двузначных чисел
• Урок 5. Опорное число при умножении чисел до 100
• Урок 6. Умножаем любые числа до 100
• Урок 7. Возведение в квадрат

Дополнительные материалы. Тренировка. В дополнение к урокам на сайте представлены многочисленные приемы и способы, упражнения, методики, интересные примеры, статьи и видео и многое другое для тренировки и развития вашего быстрого счета в уме.

Уже сейчас вы можете проверить, как быстро вы считаете в уме.

Евгений Буянов

Как быстро складывать числа в уме, тренировка устного счета 2 класс

Зачем помнить, если вы решите любую арифметическую проблему, которую вы можете сделать на калькуляторе. Современная медицина и психология доказывают, что речевой учет — это тренировка для серых клеток. Реализация такой гимнастики необходима для развития памяти и математических навыков.

Существует множество способов упрощения вычислений.

Любой, кто видел знаменитый «Устный счет» Богданов-Бельский, всегда удивлен — как дети сельского хозяйства могут решить такую ​​трудную задачу, поскольку они разделяют сумму пяти чисел, которые должны быть квадратными в первую очередь?

Оказалось, что эти дети являются учениками знаменитого учителя математики Сергея Александровича Рачицкого (также показано на картинке).

Это не детские вундеркинды — ученики основных классов деревни в XIX веке. Century. Но все уже знают методы упрощения арифметических вычислений и обучения таблиц умножения! Поэтому эта проблема может быть решена этими детьми!

Секреты устного счета

Существуют методы устного счета — Простые алгоритмы, которые желательно придать автоматизму.

Освоив простые методы, вы можете продолжать освоить более сложные задачи.

Добавление номеров 7,8,9

Чтобы упростить вычисление числа 7,8,9, вы должны сначала около 10, а затем вычесть увеличение. Например, если вы хотите добавить 9 двузначных чисел, вы должны сначала добавить 10, затем вычесть 1 и так далее.

примеров:

56 + 7 = 56 + 10-3 = 63

47 + 8 = 47 + 10-2 = 55

73 + 9 = 73 + 10-1 = 82

Быстрое добавление двузначных чисел

Если последняя цифра двузначного числа больше пяти, поверните ее вверх.

Мы выполняем добавку, и мы выводим «добавку» из полученной суммы.

примеров:

54 + 39 = 54 + 40-1 = 93

26 + 38 = 26 + 40-2 = 64

Если последняя цифра двузначного числа меньше пяти, добавьте ее к номерам: сначала добавьте дюжину, затем — единицы.

пример::

57 + 32 = 57 + 30 + 2 = 89

Если суммы будут обменены, вы можете сначала округлить число от 57 до 60, а затем вычесть из общей суммы 3:

32 + 57 = 32 + 60-3 = 89

У нас есть трехзначные числа

Можно ли быстро вычислить и добавить трехзначные числа?

Да. Чтобы сделать это, мы должны разделить трехзначные числа на сотни, десятки, единицы и добавить их взамен.

пример::

249 + 533 = (200 + 500) + (40 + 30) + (9 + 3) = 782

Характеристики обратного отсчета: сокращение до округлых чисел

Перерасход округляется до 10 — 100. Если вам нужно вычесть двузначное число, вы должны округлить его до 100, вычесть, а затем добавить исправление для остальных.

Это важно, если изменение невелико.

примеров:

67-9 = 67-10 + 1 = 58

576-88 = 576-100 + 12 = 488

Подсчитайте трехзначные числа в своем уме

Если своевременный состав чисел от 1 до 10 был хорошо управляемым, вычитание может выполняться по частям и последовательностям: сотни, десятки, единицы.

пример::

843-596 = 843-500-90-6 = 343-90-6 = 253-6 = 247

Умножать и делиться

Сразу же размножаться и делиться мыслями?

Это возможно, но не зная таблицу умножения, это незаменимо. Таблица умножения — это золотой ключ для быстрого вычисления в духе! Он используется как для воспроизведения, так и для разделения.

Напомним, что дети в начальных классах деревни в дореволюционной Смоленской губернии (картина «глаголитическая учетная запись») знали, что они продолжают таблицу умножения — с 11 до 19!

Хотя, на мой взгляд, достаточно знать таблицы с 1 по 10, чтобы мы могли умножать большее число. Например,:

15 * 16 = 15 * 10 + (10 * 6 + 5 * 6) = 150 + 60 + 30 = 240

Умножьте и разделите на 4, 6, 8, 9

Освоив умножение таблицы на 2 и 3 на автоматизацию, упростите другие вычисления.

Мы используем простые методы для умножения и разбиения двух- и трехзначных чисел:

• умножить на 4 — умножить на 2;

• умножить на 6 — это означает умножение на 2, затем на 3;

• умножить на 8 — умножить на 3 раза на 2;

• умножить на 9 — умножить на 3 раза.

Например,:

37 * 4 = (37 * 2) * 2 = 74 * 2 = 148;

412 * 6 = (412 * 2) · 3 = 824 · 3 = 2472

аналогичным образом,

• доля с 4 — это дважды делится на 2;

• доля с 6 — это сначала делится на 2, затем с 3;

• разделите на 8 — это три раза поделено на 2;

• доля с 9 — это дважды делится на 3.

Например,:

412: 4 = (412: 2): 2 = 206: 2 = 103

312: 6 = (312: 2): 3 = 156: 3 = 52

Как умножить и разделить на 5

Число 5 равно половине 10 (10: 2).

Поэтому умножьте на 10, затем разделите его на половину.

пример::

326 * 5 = (326 × 10): 2 = 3260: 2 = 1630

Правило разделения в 5 еще проще. Сначала умножьте на 2, а затем разделите на 10.

326: 5 = (326 * 2): 10 = 652: 10 = 65,2.

Умножение на 9

Если вы хотите умножить число на 9, вам не нужно удвоить его на 3.

Достаточно умножить его на 10 и вычесть умноженное число. Сравните это быстрее:

37 * 9 = (37 * 3) * 3 = 111 * 3 = 333

или

37 * 9 = 37 * 10-37 = 370-37 = 333

Кроме того, частные образцы, которые значительно упрощают воспроизведение двузначных чисел на 11 или 101, уже давно наблюдаются, поэтому при умножении на 11 двузначных чисел перемещаются. Компоненты его чисел остаются на краях, а сумма — центром.

Например: 24 * 11 = 264. При умножении на 101 достаточно двузначное число присваивается одинаково. 24 * 101 = 2424. Простота и последовательность таких случаев замечательна. Такие проблемы очень редки — это забавные случаи, так называемые маленькие трюки.

Подсчет пальцев

Сегодня вы все еще можете увидеть много сторонников «физкультуры пальцев» и техники устных счетов на пальцах.

Мы убеждены, что это очень очевидно и удобно, если мы научимся складывать и отбирать, сгибать и сгибать пальцы. Степень таких расчетов очень ограничена. Как только вычисления превышают масштаб одной операции, возникают проблемы: нужно освоить следующий метод. Да, и сгибание пальцев в эпоху iPhones является своего рода неустойчивым.

Например, в поддержку техники «пальца» дается умножение на 9.

Уловка при принятии:

• Если вы хотите умножить число в первой десятке на 9, вам нужно расширить свою ладонь самостоятельно.
• Нумеруя слева направо, согните палец, соответствующий умноженному числу. Например, если вы хотите умножить 5 на 9, вам нужно согнуть маленький палец с левой стороны.
• Оставшееся количество пальцев слева будет соответствовать десяти, справа — на юнитах. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.

Это правда, что решение является быстрым и визуальным! Но это из области трюков.

Правило работает, только если оно умножено на 9. Не проще ли умножить 5 на 9, чтобы узнать таблицу умножения? Этот фокус будет забыт, и хорошо изученная таблица умножения останется навсегда.

Кроме того, существует много других таких методов, использующих пальцы для некоторых отдельных математических операций, но это факт, пока вы его используете и сразу забываете, когда перестаете его использовать. Поэтому лучше изучить стандартные алгоритмы, которые будут длиться всю жизнь. 

Устный счет на машине

• Вы должны сначала знать состав и умножение.

• Во-вторых, нам нужно запомнить методы упрощения вычислений.

  Секреты волшебства математики. Как научиться быстро читать.

  Как оказалось, таких математических алгоритмов не так много.

• В-третьих, для того, чтобы стать удобной техникой, необходимо провести короткий «мозговой штурм» сеансов — выполнение устных расчетов с использованием одного или другого алгоритма.

Обучение должно быть кратким: решить в 3-4 случаях, используя ту же технику, затем перейти к другой.

Необходимо попытаться использовать любые бесплатные минуты — полезные и скучные. Благодаря простому обучению все вычисления будут выполняться с молниеносной скоростью без ошибок.

Это очень полезно в жизни и поможет в сложных ситуациях.

Урок 3. Традиционное умножение в духе

Давайте посмотрим, как вы можете умножить двузначные числа на традиционные методы, которые учат нас в школе. Некоторые из этих методов позволяют быстро продублировать двузначные числа при достаточной подготовке.

Знание этих методов полезно. Однако важно понимать, что это только верхушка айсберга. Этот урок учитывает самые популярные методы умножения для двузначных чисел.

Первый маршрут — набор для десятков и единиц

Самый простой способ понять умножение двузначных чисел — это тот, который мы узнали в школе.

Он составлен таким образом, что оба фактора делятся на десятки и те, а затем умножают полученные четыре числа.

Насколько реалистично быстро учиться?

Этот метод довольно прост, но требует, чтобы он сохранял до трех цифр в памяти и одновременно выполнял арифметические операции.

Например: 63 * 85 = (60 + 3) * (80 + 5) = 60 * 80 + 60 * 5 + 3 * 80 + 3 * 5 = 4800 + 300 + 240 + 15 = 5355

Более простые такие случаи решаются в трех действиях. Во-первых, умножьте десятки друг на друга.

Затем добавьте 2 штуки к десяткам. Затем добавляется продукт единиц. Схема может быть описана следующим образом:

• Первое действие: 60 * 80 = 4800 — не забывайте
• Второе действие: 60 * 5 + 3 * 80 = 540 — не забывайте
• Третье действие: (4800 + 540) + 3 * 5 = 5355 — ответ

Для быстрого эффекта вам нужно хорошее знание таблицы умножения с числами до 10, возможность добавления чисел (до трех цифр) и возможность быстрого перехода внимания от одной кампании к другой с учетом предыдущего результата.

Последний навык подходит для обучения, отображая арифметические операции, когда вам нужно визуализировать образ вашего решения и промежуточные результаты.

Заключение. Нетрудно видеть, является ли этот метод не самым эффективным, то есть разрешить правильный результат в наименьших действиях. Следует также принимать во внимание другие способы.

Второй метод — арифметическая ошибка

Рассмотрение дела в соответствующей форме является довольно распространенным способом учета в памяти.

Настройка случая подходит, когда вам нужно быстро найти приблизительный или точный ответ. Желание адаптировать случаи при определенных математических моделях часто поднимает математические стулья в университетах или школах классов с математическим уклоном. Люди учатся находить простые и удобные алгоритмы для решения различных задач.

Вот несколько примеров установки:

Пример 49 * 49 можно решить следующим образом: (49 * 100) / 2-49. Во-первых, 49 считается сто-4900. Затем 4900 делится на 2, что составляет 2450, а затем вычитается 49.

Продукт 56 * 92 был решен следующим образом: 56 * 100-56 * 2 * 2 * 2. Оказалось: 56 * 2 = 112 * 2 = 224 * 2 = 448. Из 5600 мы вычитаем 448, получим 5152.

Этот метод может быть более эффективным, чем предыдущий, только если у вас есть устная учетная запись, основанная на умножении двузначных чисел на отдельные цифры и в то же время она может содержать несколько результатов.

Кроме того, вам нужно потратить некоторое время на поиск алгоритма решения, и большое внимание уделяется надлежащему рассмотрению этого алгоритма.

Заключение. Способ, которым вы пытаетесь умножить два числа, поставив простые арифметические процедуры и тренировав свой мозг, но связанный с большими психическими издержками и риском получения неправильного результата, выше, чем в первом режиме.

Третий метод — это ментальная визуализация умножения в столбце

56 * 67 — мы будем считать в столбце.

Вероятно, количество столбцов содержит максимальное количество действий и требует постоянного внимания к вспомогательным номерам.

Однако его можно упростить. Во втором уроке было сказано, что важно, чтобы мы могли быстро умножать отдельные цифры в двузначных числах. Если вы уже знаете, как это сделать на машине, учетная запись в соответствующем столбце будет не так сложна для вас. Алгоритм выглядит следующим образом

Первое действие: 56 * 7 = 350 + 42 = 392 — помните и не забывайте о третьем акте.

Второе действие: 56 * 6 = 300 + 36 = 336 (хорошее или 392-56)

Третье действие: 336 * 10 + 392 = 3360 + 392 = 3 752 — здесь сложнее, но вы можете начать называть первое число, в котором вы уверены — «три тысячи …», но на данный момент установлены 360 и 392.

Вывод: Учетная запись в столбце напрямую сложна, но может быть, если у вас есть навыки быстрого двойного двузначного числа с одним значением, чтобы упростить его.

Добавьте к этому арсенал и этот метод. В упрощенной форме число в столбце изменяет один из первых методов. Что лучше — вопрос для любителя.

Как вы можете видеть, ни один из описанных методов не позволяет достаточно быстро и точно учитывать все случаи умножения двузначных чисел. Следует понимать, что использование традиционных методов умножения для учетной записи не всегда рационально, что наименьшее усилие состоит в достижении максимальных результатов.

← ← 2 Простая арифметика4 Специальные методы →

Как научиться быстро считать в уме сложные числа

Методика «Умение считать в уме»

С помощью данной методики проверяется способность ре­бенка производить умственные арифметические действия с чис­лами и дробями разного типа: простыми и десятичными, а так­же со сложными, дробно-целыми числами. Если ребенка научи­ли считать еще до поступления в школу, то данную методику можно применять, начиная с дошкольного возраста.

В норме же она служит для оценки соответствующей способности у детей, уже обучающихся в школе.

Примеры на счет (табл. 6) предлагаются ребенку на слух в порядке их усложнения. Он должен как можно быстрее сосчи­тать в уме и дать устный ответ.

В таблице справа и слева приведены баллы, которыми оце­нивается правильное решение того или иного арифметического примера.

Все примеры в таблице разделены на группы. Если из данной группы, включающей три примера, ребенок решил не ме­нее двух примеров, то ему приписывается определенный балл. Группы примеров, оцениваемых соответствующим количеством баллов, отделены в таблице друг от друга отрезками горизонталь­ных линий. Между ними находятся те оценки, которые получа­ет ребенок за правильное решение данных примеров.

Общее время, отводимое на выполнение всего задания (решение 48 примеров), равно 5 минутам.

Задание заключается в том, чтобы за это время решить как можно больше примеров.

Примеры для устного счёта к методике * Умение считать в уме»

а баллах	Примеры (с порядковыми номерами и решениями)	Оценка в баллах
0,8	0,1	1.5 + 2-7 25.0,83 + 0,12-0,95 2. Как быстро считать в уме: приемы устного счета больших чисел 4 +5 — 9 26.0,47 + 0,35 = 0,82 3. 6 — 2 — 4 27.0,22 — 0,13 = 0,09	0,7	3,2
0,2	4.9 — 6 — 3 28.0,87 — 0,43 = 0,44 5.3( 2-6 29.0,22( 0,1 -0,022 6. 2 ( 4 = 8 30.0,15 ( 0,2-0,03	0,8
0,2	7.9:3-3 31.0,21:0,1 = 2,1 8. 6:2 — 3 32.0,48:0,24 — 2,0 9.10 + 6= 16 33.1/4 + 1/4 = 1/2	0,8
0,3	10.12 + 4=16 34.1/4 + 2/4 = 3/4 11.16-4- 12 35.3/5+1/8 = 29/40 12.19-7- 12 36.9/16-5/16= 1/4	0,9
1,6	0,3	13.4( 3- 12 37.1/3( 1/3- 1/9 14. 6 ( 3= 18 38. 2/8 ( 3/8 — 3/32 15.18:3 — 6 39.4/5:2/5 — 2,0	0,9	2,0 2,4
0,4	16.15:5 = 3 40.5/16:3/16 = 5/3 17.25 + 32 = 57 41.1/2 + 2/4= 1,0 18.41 +23-64 42.8/32 + 3/4= 1,0	1,1
0,4	19.43 — 17 — 26 43.9/10 — 2/5 = 1/2 20.67-21 =46 44. 9/16-3/4 = -3/16 21.16( 5-80 45.2/6( 1/2- 1/6	1,1
0,5	22. 22 ( 4 = 88 46.3/16 ( 3/4 = 9/64 23.48 :12 — 4 47.4/12:2/3 = 1/2 24.84:14 = 6 48.8/32:4/16=1	1,3

Правильные решения, данные в самих примерах, должны быть известны только экспериментатору и служат для него сред­ством контроля решения, предложенного ребенком.

Сумма баллов, полученных ребенком за правильно решен­ные в течение 5 минут примеры, является тем показателем, который затем переводится в баллы по стандартизированной 10- балльной шкале.

Выводы об уровне развития

7,7 балла и выше — очень высокий.

от 5,7 до 7,6 балла — высокий,

от 2,5 до 5,6 балла — средний,

от 0,9 до 2, 4 балла — низкий,

меньше 0,8 балла — очень низкий.

Интерпретация полученных результатов производится следующим образом (приводимый пример касается учащихся 1у классов средней школы; способы оценки умения считать в уме у детей других возрастов еще предстоит уточнить с учетом про- граммы по математике, по которой они обучаются в школе).

Сумма баллов, находящаяся в пределах от 7,7 до 10,0, счита­ется очень хорошим результатом и свидетельствует о наличии у ребенка способностей к математике.

Сумма баллов в пределах от 5,7 до 7,6 рассматривается как хороший результат и говорит о средних способностях данного ребенка.

Сумма баллов, оказавшаяся в интервале от 2,5 до 5,6 балла, свидетельствует о наличии у данного ребенка слабых способнос­тей к математике.

Сумма баллов, расположенная в пределах интервала от 0,9 до 2,4, является признаком том, что способности к усвоению ма­тематики у данного ребенка полностью отсутствуют.

Результат, меньший 0,8 баллов, является признаком серьез­ного отставания развития математического мышления у ребенка.

«ИСКЛЮЧЕНИЕ СЛОВ»

Методика предназначена для оценки вербально-логического мышления: способность ребенка к обобщению и выделению существенных признаков.

Приводится по книге Е.И. Рогова(1995,с74).

Материал. Бланк методики «Исключение слов», содержащий 15 заданий, каждое из пых содержит по 4 слова; секундомер и протокол (табл.

16) для регистрации ответов.

Таблица 16



Устный счет: как научиться считать в уме

Активируйте PRO-подписку, чтобы проходить курс эффективнее

«Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов.

Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят вам научиться организовывать себя в различных жизненных ситуациях.

Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».

Тренировка устного счета

Есть люди, которые умеют совершать несложные арифметические операции в уме.

Умножить двузначное число на однозначное, умножать в пределах 20, перемножить два небольших двузначных числа и т.д. – все эти действия они могут производить в уме и достаточно быстро, быстрее среднего человека. Часто этот навык оправдан необходимостью постоянного практического использования.

Как правило, люди, которые хорошо считают в уме, имеют математическое образование или, по крайней мере, опыт решения многочисленных арифметических задач.

Несомненно, опыт и тренировка играет важнейшую роль в развитии любых способностей.

Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые, в отличие от вышеописанных, способны считать в уме гораздо более сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать сложные арифметические операции, которые не каждый человек и в столбик сможет посчитать.

Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью?

На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме. Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно.

Как научиться ребенку быстро считать в уме?

Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета.

Нужно отметить, что третий фактор имеет ключевое значение.

Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете «переплюнуть» даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Уроки на сайте

Уроки устного счета, представленные на сайте, направлены именно на развитие этих трех составляющих.

В первом уроке рассказано, как развить в себе предрасположенность к математике и арифметике, а также описаны основы счета и логики. Затем дан ряд уроков по специальным алгоритмам для совершения различных арифметических операций в уме. И наконец, в данном тренинге представлены дополнительные материалы, помогающие тренировать и развивать умение считать устно, для того, чтобы суметь применить свой талант и свои знания в жизни.

Урок 1. Способности. Упражнения и рекомендации по развитию устного счета, внимания, краткосрочной памяти.

Уроки 2-7. Алгоритмы. Что касается методик, то они даны в следующих уроках, которые разделены на несколько видов:

Дополнительные материалы. Тренировка. В дополнение к урокам на сайте представлены многочисленные приемы и способы, упражнения, методики, интересные примеры, статьи и видео и многое другое для тренировки и развития вашего быстрого счета в уме.

Уже сейчас вы можете проверить, как быстро вы считаете в уме.

Cтатистика На весь экран

1 Внимание и концентрация →