Рисование разноцветные мыльные пузыри. Рисование мыльными пузырями – мастер-класс. Этапы выполнения работы
Муниципальное автономное общеобразовательное учреждение
«Школа-интернат №31» — МАОУ «ШИ № 31».
456227 Челябинская область, г. Златоуст, поселок Айский, д. 20-б
Тел. факс 8 3513 – 79-12-31 E — mail : shkola [email protected] list . ru
Мастер-класс
«Рисование мыльными пузырями»
Вачаева Юлия Фёдоровна
Воспитатель
г. Златоуст
Тема: Рисование мыльными пузырями
Цель мастер – класса: познакомить педагогов с нетрадиционной художественной техникой – рисование мыльными пузырьками.
Задачи мастер – класса:
Раскрыть для педагогов новый способ развивать у детей с умственной отсталостью абстрактное мышление, ассоциативное воображение, цветовосприятие.
Как метод взаимодействия с учениками в ходе занятия поощрять детское творчество, инициативу.
Формировать умение находить в своем необычном рисунке художественный образ, дополнять его нужными деталями.
Оборудование
вода
моющее средство: жидкое мыло, детский шампунь, гель для душа и т.д.
красители: пищевые (предпочтительнее, потому что в этом случае узоры получаются более тонкими и ажурными) или гуашь
коктейльные трубочки, ложки
плотная бумага
Орг. момент: Мыльные пузыри — известная детская забава. Хрупкие, прозрачные, они так красиво переливаются разными цветами радуги и создают ощущение праздника. И еще ими можно рисовать.
Рисунки в этой необычной технике тоже оказываются очень необычными, а занятие приносит детям радость. К тому же, отпечатки каждый раз получаются разными, поэтому очень интересно с ними экспериментировать, а потом фантазировать, на что они похожи.
Основной этап: Как рисовать мыльными пузырями. Мастер-класс
Этапы работы
Сделать раствор для мыльных пузырей. Для этого смешать воду и моющее средство примерно в отношении 5:1. Добавить красители.
Для этого смешать воду и моющее средство примерно в отношении 5:1. Добавить красители.
Коктейльной трубочкой взболтать раствор, а затем, не вынимая из раствора трубочку, подуть в нее, чтобы раствор начал пузыриться. Рисовать можно, прикладывая бумагу к пузырящемуся раствору или выкладывая его на бумагу ложкой.
На одном и том же листе можно рисовать мыльными пузырями разных цветов так, чтобы они накладывались друг на друга, или создавая отдельные отпечатки на расстоянии друг от друга.
Попробуйте перелить готовый раствор в глубокую тарелку, чашку или миску, чтобы круги-отпечатки получались большими
.
Использование бумаги с такими рисункам
Полученную разноцветную бумагу с необычными узорами можно использовать любым из следующих способов:
как фон для открыток, рисунков, аппликаций
для упаковки подарков, подарочного пакетика .
превращать отпечатки в разных существ или предметы, дорисовывая необходимые детали (как в монотипии или кляксографии)
Рефлексия: Надеюсь, мой мастер – класс оказался для вас полезным и интересным. С радостью выслушаю ваши вопросы и дам на них ответы.
С радостью выслушаю ваши вопросы и дам на них ответы.
Приятного Вам творчества!
Всего доброго!
Мыльные пузыри – любимая игрушка огромного количества детей. Мальчики и девочки с удовольствием дуют на специальную палочку, выдувая переливающиеся шарики разного размера, а также догоняют их и пытаются поймать.
Между тем, это далеко не единственное применение этого уникального состава на мыльной основе. Сегодня все больше взрослых и детей осваивают технику рисования мыльными пузырями, с помощью которой можно создавать оригинальные шедевры. Делать это совсем не сложно, хотя в первый раз может показаться, что для такого требуются специальные навыки.
В данной статье мы расскажем вам, что представляет собой рисование мыльными пузырями для детей, и какие материалы вам потребуются для создания уникальных шедевров в этой технике.
Как научиться рисовать мыльными пузырями на бумаге?
Чтобы научиться рисовать в этой необычной технике, подготовьте флакон с который можно приобрести в любом детском магазине, яркие краски разных цветов, подходящие стаканчики и акварельную бумагу.
В принципе, можно использовать и обыкновенную бумагу для рисования, но именно на акварельной картинки получаются необычайно яркими и красивыми. В один из стаканчиков налейте чистую воду, а во все остальные разлейте мыльную основу для выдувания мыльных пузырей. В каждую из емкостей с этим раствором налейте небольшое количество краски и хорошо перемешайте.
В состав жидкости для рисования мыльными пузырями не должно входить ничего, кроме мыльной основы и краски, причем последней должно быть совсем немного. Если концентрация красящего вещества будет слишком большой, создать красивый рисунок не получится. Приготовив мыльную воду определенного цвета, возьмите соломинку и дуньте через нее так, чтобы в стаканчике образовалось как можно больше пузырей.
Сразу после этого приложите сверху к этой емкости лист акварельной бумаги – на нем останутся яркие абстрактные узоры.
Когда техника получения изображения будет освоена, можно приступать и к рисованию рисунков с использованием мыльных пузырей. Для этого вам потребуется трубочка для их выдувания, которая продается в комплекте с мыльной основой. Лучше всего использовать несколько трубочек – по одной на каждый оттенок краски. Если у вас только один инструмент, вам придется мыть его после каждого применения.
Для этого вам потребуется трубочка для их выдувания, которая продается в комплекте с мыльной основой. Лучше всего использовать несколько трубочек – по одной на каждый оттенок краски. Если у вас только один инструмент, вам придется мыть его после каждого применения.
Приготовив все необходимые материалы и приспособления, начинайте выдувать разноцветные пузыри на лист акварельной бумаги. После небольшой тренировки вы научитесь создавать в этой необычной технике не только абстрактные изображения, но и оригинальные рисунки, которые можно будет использовать для украшения интерьера или подарить близким.
Вот, что может у вас получиться, если вы всерьез увлечетесь этим занятием.
Нет ничего столь легкого, хрупкого и необычайно привлекательно для детей как мыльные пузыри . Они – неотъемлемый символ детства уже много поколений.
Помните, как взбалтывали в металлических тубах мыльную воду и соревновались, у кого пузырь выйдет больше и продержится дольше? А догадывались ли вы, что использовать их можно не только в качестве игры, но и в творчестве, например, рисовании? Сегодня мы подготовили необычный мастер-класс , который поможет вам по-новому взглянуть на привычные свойства

Готовим материалы: воду, тарелки разной глубины, но диаметром не больше альбомного листа, моющее средство («Фейри»), краски (гуашь), несколько коктейльных трубочек и пару пластмассовых ножичков (стеков).
Следующий шаг – подготовка краски. В тарелке соединяем 1 ч.л. воды, 1 ч.л. фейри, 0,5 ч.л. краски. Используйте разные цвета, однако можем посоветовать не брать для работы желтую краску, а также не использовать акварель, поскольку свойства краски отличаются от гуаши.
Самый ответственный момент – выдуваем пузыри! Если ребенок еще мал, то лучше это сделать взрослым, чтобы малыш ненароком не вдохнул краску в себя. Попробуйте раздуть пузыри так, чтобы цветная мыльная шапка поднималась выше края тарелки.
А теперь накройте тарелку листом бумаги. Лопнувшие пузыри оставят на ней удивительные следы. Пусть лист высохнет.
Различные сочетания цветов и дадут вам необыкновенные фоны, которые мы можем использовать для дальнейшего рисования или для декора бумаги. Из листов, украшенных таким способом, можно изготовить оригинальную упаковку для подарка, например.
Из листов, украшенных таким способом, можно изготовить оригинальную упаковку для подарка, например.
Отпечатки пузырей, неповторяющиеся как отпечатки пальцев, прекрасно подстегнут фантазию как детей, так и взрослых. Сколько фигур можно увидеть в них: и кота, и букет, и дом, и дерево. Осталось только проявить силуэт или добавить своих деталей – и рисунок готов!
Подобное задание развивает воображение, творческий подход. Покрутите лист вокруг оси, возможно, с другого ракурса вы увидите совсем другие фигуры, надо только приглядеться.
Елена Копченова
Мыльные пузыри – переливающиеся всеми цветами радуги, всегда вызывают улыбку и восторг. А вы знаете, что
Что необходимо для работы : вода в баночке, детский шампунь или
жидкое мыло, гуашь,акварель или пищевые красители,плотная бумага, трубочки для коктейля, ложечка.
В воду добавьте шампунь или жидкое мыло. Концентрация примерно 1 :10 (не строго) . Чтобы пузыри были большими и подолгу не лопались, добавьте в воду чуть-чуть желатина или глицерина. Все ингредиенты перемешайте и оставьте постоять на 2-3 дня. Затем профильтруйте раствор через марлю и оставьте в холодильник на 12 часов. Процедуру можно упростить — просто добавив в воду мыльный раствор и красители .
Чем больше красителя, тем ярче цвет пузырей .
Все, теперь можно создавать красивые воздушные шары.
1 способ. Берем соломинку для коктейля и начинаем пенить раствор (дуем в трубочку, чтобы пузыри поднялись в баночке . Когда пена поднялась, берем плотную бумагу и прислоняем ее к мыльной пене .
2 способ. Можно снимать поднявшиеся пузыри ложкой и выкладывать на листе.
Таким образом, можно одним листом бумаги пройтись по всем цветам.
А теперь начинаем всматриваться в узоры мыльных пузырей и фантазировать , дорисовывать .
А можно вырезать узор мыльного пузыря и использовать в аппликации.
Используя эти два способа можно получить интересные работы. Судите сами.
Если вы хотите чтобы ваш ребенок вырос инициативным, разносторонним, умел принимать необычные решения, тогда надо развивать творческое воображение.
Для этого отлично подойдут обычные мыльные пузыри, но не в обычном применении. Будем рисовать этими забавными шариками.
Рисование мыльными пузырями улучшает творческую фантазию, помогает видеть сходства между, на первый взгляд, ничем не похожими предметами.
Не стоит забывать и о том, что такой способ не традиционного рисования, доставляет массу положительных эмоций для детей.
Для рисования мыльными пузырями потребуется:
- Одноразовые стаканы;
- Листы плотной бумаги;
- Гуашь или пищевые красители;
- Раствор мыльных пузырей;
- Коктейльные палочки;
- Одноразовая ложка;
- Карандаши или фломастеры.

Если нет готовых мыльных пузырей, то можно воспользоваться простым рецептом раствора.
Рецепт: 1 часть воды + 1 часть жидкого мыла (детский шампунь).
Возьмите одноразовые стаканчики, столько штук, сколько у Вас будет цветов. Один стакан – один цвет.
Смешайте в стакане воду с жидким мылом. Затем добавьте красители.
Чем больше красителя, тем красочней будут цвета.
Идеальные, сочные и яркие цвета получатся, если составить мыльный раствор в таких пропорциях: 5 частей гуаши + 1 часть воды + 1 часть жидкого мыла.
Есть один момент, на котором стоит заострить свое внимание, это брызги при выдувании пузырей. Поэтому на стол кладем клееночку, а на ребенка старенькую одежду.
После того как смешали раствор для рисования, берем трубочку для коктейля и вставляем в стаканчик, после начинаем «выдувать» раствор. Когда пена из мыльных пузырей будет выходить за края стакана, то берем бумагу и прикладываем ее к мыльной пене.
Еще есть вариант, снимать пенку из мыльных пузырей ложечкой или палочкой, после чего пену и положить на бумагу.
Так же можно воспользоваться трафаретом, или вырезанным шаблоном. Положить шаблон сверху листа, на котором рисует ребенок. И заполнить мыльным раствором.
Смотрим на получившиеся отпечатки и включаем фантазию, представляем, воображаем, что получилось. Осталось только дорисовать. И все чудесная картина готова.
Видео рисование мыльными пузырями
Опыт «Мыльные пузыри Фиксики»
Фикси-опыт «Мыльные пузыри» порадует вашего ребёнка и позволит ему надувать самые разнообразные пузыри. Опыт на 100% безопасен, он надолго заинтересует вашего ребёнка. В комплект для этого зрелищного опыта входят инструкция по применению, мыльный раствор и пластмассовые детали для пускания мыльных пузырей (воздушный шар, воронка, лоток, блюдце и т.п.).
Рекомендовано детям от 3-х лет.
Смотрите так же:
Мастер-класс «Нетрадиционная техника рисования мыльными пузырями»
Мастер-класс «Нетрадиционная техника. Мыльные пузыри».
Мыльные пузыри».
— Добрый день уважаемые коллеги. Предлагаю Вашему, вниманию мастер-класс на тему: «Нетрадиционная техника. Мыльные пузыри».
Нет более безнадежного занятия, чем рисовать пустоту, нет ничего труднее, как живописать однообразие.
Стефан Цвейг
— Все мы знаем, что рисование одно из самых больших удовольствий для ребенка. В рисовании раскрывается его внутренний мир. Рисуя, ребенок отражает не только то, что видит вокруг, но и проявляет собственную фантазию.
— Нестандартные подходы к организации изобразительной деятельности удивляют и восхищают детей, тем самым, вызывая стремление заниматься таким интересным делом. Нетрадиционное рисование раскрывает креативные возможности ребенка, позволяет почувствовать краски, их характер и настроение.
— Уважаемые воспитатели, как вы думаете, что может обозначать слово нетрадиционно? (ответы воспитателей) Нетрадиционно — не основываясь на традиции. Происходя не в силу установившейся традиции, устраиваясь не по заведенному обычаю. Отличаясь оригинальностью. Не придерживаясь традиций.
— Нетрадиционное рисование – это искусство изображать, не основываясь на традиции.
— Рисование нетрадиционными способами, увлекательная, завораживающая деятельность, которая удивляет и восхищает детей. Учёными изучено и освоено более 30 различных техник рисования:
техника тычка;
рисование пальчиками;
рисование ладошкой;
оттиск пробкой, печатками, ластиком;
оттиск поролоном, пенопластом;
оттиск смятой бумагой;
обрывание бумаги;
скатывание бумаги;
рисование восковыми мелками и акварелью;
рисование акварелью и свечой;
монотипия приоритетов;
монотипия пейзажная;
кляксография;
набрызг;
тиснение;
тычкование;
цветной граттаж;
черно-белый граттаж;
рисование акварельными мелками;
рисование нитками;
рисование с помощью мыльных пузырей;
рисование пластилином;
рисование солью;
рисование опилками.
— Рисование необычными материалами и оригинальными техниками позволяет детям ощутить незабываемые положительные эмоции. Каждая из этих техник — это маленькая игра. Их использование позволяет детям чувствовать себя раскованнее, смелее, непосредственнее, развивает воображение, дает полную свободу для самовыражения.
— А сейчас, предлагаю, Вам, окунуться в детство и попробовать порисовать мыльными пузырями.
— Мыльные пузыри – переливающиеся всеми цветами радуги, всегда вызывают улыбку и восторг. Это очень интересная техника, она порадует и взрослых, и детей. Можно не только дуть пузыри, но и делать их цветными, переносить на бумагу, рисовать удивительные рисунки, изготавливать аппликации.
Что необходимо для работы: вода в баночке, детский шампунь, жидкое моющее средство или жидкое мыло, гуашь, акварель или пищевые красители, плотная бумага акварельная, трубочки для коктейля, ложечка, баночка с мыльными пузырями (нам понадобится трубочка с кольцом).
В воду добавьте шампунь или жидкое мыло. Концентрация воды и мыла примерно 1:10 (не строго). Чтобы пузыри были большими и подолгу не лопались, добавьте в воду чуть-чуть желатина или глицерина. Все ингредиенты перемешайте и оставьте постоять на 1-2 дня. Затем добавьте гуашь, акварель или красители.
Чем больше красителя, тем ярче цвет пузырей.
Все, теперь можно создавать красивые воздушные шары.
1 способ. Берем соломинку для коктейля и начинаем пенить раствор (дуем в трубочку, чтобы пузыри поднялись в баночке). Когда пена поднялась, берем плотную бумагу и прислоняем ее к мыльной пене.
2 способ. Можно снимать поднявшиеся пузыри ложкой и выкладывать на листе.
3 способ. С помощью кольца от купленных мыльных пузырей получаются немного другие по форме отпечатки мыльных пузыриков. Они ровные и четкие.
Они ровные и четкие.
Таким образом, можно одним листом бумаги пройтись по всем цветам.
В результате у вас получатся случайные абстрактные разноцветные узоры
Пузыри должны высохнуть.
А теперь начинаем всматриваться в узоры мыльных пузырей и фантазировать, дорисовывать.
А можно вырезать узор мыльного пузыря и использовать в аппликации.
Используя эти три способа можно получить интересные работы.
Практическая деятельность.
Рефлексия.
— Скажите, пожалуйста, Вам было интересно?
— Может, кто-нибудь хочет поделиться своими впечатлениями?
— Было очень приятно всех видеть, спасибо за внимание.
Творческих Вам находок!
Мастер-класс для педагогов ДОУ «Нетрадиционная техника. Мыльные пузыри».
Подготовила: старший воспитатель Н. В. Никишанова
В. Никишанова
2018 г.
Мастер класс «Осеннее дерево» рисование мыльными пузырями | Материал по рисованию (старшая группа):
Мастер-класс для родителей и детей «Осеннее дерево»-рисование мыльными пузырями.
Провела Кружкова Д.А.
Дата: 11.11.2019
КОНСПЕКТ
Применение: мастер – класс рассчитан на старшую группу детского сада для родителей и детей.
Участники: дети, родители.
Цель: вовлечение родителей в совместную деятельность с детьми.
Знакомство с нетрадиционным методом рисования мыльными пузырями. Воспитывать интерес к творчеству. Способствовать развитию творческого воображения, мышления, художественно-эстетических навыков, мелкой моторики, глазомера, внимания.
Задачи:
1. Сформировать у родителей интерес к деятельности детей по рисованию.
2. Дать родителям представление о нетрадиционном рисовании с детьми, используемом в детском саду.
Оборудование:
— гуашь
— стаканчики с водой,
— трубочки для сока,
— кисточки,
— альбомные листы,
— шампунь или средство для мытья посуды.
Описание:
Уважаемые родители! Я очень рада видеть Вас! Наша сегодняшняя встреча необычна. Сегодня вы сможете проявить свою фантазию и творчество. Тема нашей встречи Осеннее дерево нетрадиционным способом рисования, с помощью мыльных пузырей.
Я уверена, что вы, родители рисуете с детьми, но скорее всего это карандаши и фломастеры иногда краски. Это связано с тем, что дети оставляют запачканные столы, стулья, одежду и стены. Но детям в этом возрасте необходимо рисовать красками.
Воды- обыкновенной
В стаканчик набери
Пускать из мыльной пены
Мы будем пузыри.
Этапы выполнения работы:
1. Возьмём пластиковые стаканчики,в стаканчик добавим
2- чайной ложки воды,1-чайную ложки гуаши, 2- чайные ложки жидкого мыла или жидкость для мытья посуды. Хорошо перемешать.
2. Опускаем трубочку для сока в стаканчик и начинаем дуть в неё до тех пор, пока над стаканчиком не поднимется мыльная «шапка».
Детям привычнее пить трубочек, поэтому, сначала предложите ребёнку потренироваться пускать пузыри с обычной водой, привычной и безопасной.
3. Берём лист бумаги и рисуем ствол детрева. Когда ствол подсох прикладываем к стаканчику с мыльными пузырями разного цвета. Можно так сделать несколько раз, в зависимости от вашего творческого замысла.
4. Вот такие отпечатки получаются на листе бумаги-это разноцветные листья на дереве. Нужно дать им высохнуть.
5. Вот такие у нас получились картинки.
6. Во что превратятся «мыльные» шарики зависит от вашего творческого воображения. Спасибо за внимание!
Урок рисования мыльными пузырями. Мастер — класс по нетрадиционному рисованию
Муниципальное автономное общеобразовательное учреждение
«Школа-интернат №31» — МАОУ «ШИ № 31».
456227 Челябинская область, г. Златоуст, поселок Айский, д. 20-б
Тел. факс 8 3513 – 79-12-31 E — mail : shkola [email protected] list . ru
Мастер-класс
«Рисование мыльными пузырями»
Вачаева Юлия Фёдоровна
Воспитатель
г. Златоуст
Тема: Рисование мыльными пузырями
Цель мастер – класса: познакомить педагогов с нетрадиционной художественной техникой – рисование мыльными пузырьками.
Задачи мастер – класса:
Раскрыть для педагогов новый способ развивать у детей с умственной отсталостью абстрактное мышление, ассоциативное воображение, цветовосприятие.
Как метод взаимодействия с учениками в ходе занятия поощрять детское творчество, инициативу.
Формировать умение находить в своем необычном рисунке художественный образ, дополнять его нужными деталями.
Оборудование
вода
моющее средство: жидкое мыло, детский шампунь, гель для душа и т.д.
красители: пищевые (предпочтительнее, потому что в этом случае узоры получаются более тонкими и ажурными) или гуашь
коктейльные трубочки, ложки
плотная бумага
Орг. момент: Мыльные пузыри — известная детская забава. Хрупкие, прозрачные, они так красиво переливаются разными цветами радуги и создают ощущение праздника. И еще ими можно рисовать.
Рисунки в этой необычной технике тоже оказываются очень необычными, а занятие приносит детям радость. К тому же, отпечатки каждый раз получаются разными, поэтому очень интересно с ними экспериментировать, а потом фантазировать, на что они похожи.
К тому же, отпечатки каждый раз получаются разными, поэтому очень интересно с ними экспериментировать, а потом фантазировать, на что они похожи.
Основной этап: Как рисовать мыльными пузырями. Мастер-класс
Этапы работы
Сделать раствор для мыльных пузырей. Для этого смешать воду и моющее средство примерно в отношении 5:1. Добавить красители.
Коктейльной трубочкой взболтать раствор, а затем, не вынимая из раствора трубочку, подуть в нее, чтобы раствор начал пузыриться. Рисовать можно, прикладывая бумагу к пузырящемуся раствору или выкладывая его на бумагу ложкой.
На одном и том же листе можно рисовать мыльными пузырями разных цветов так, чтобы они накладывались друг на друга, или создавая отдельные отпечатки на расстоянии друг от друга.
Попробуйте перелить готовый раствор в глубокую тарелку, чашку или миску, чтобы круги-отпечатки получались большими
.
Использование бумаги с такими рисункам
Полученную разноцветную бумагу с необычными узорами можно использовать любым из следующих способов:
как фон для открыток, рисунков, аппликаций
для упаковки подарков, подарочного пакетика
.
превращать отпечатки в разных существ или предметы, дорисовывая необходимые детали (как в монотипии или кляксографии)
Рефлексия: Надеюсь, мой мастер – класс оказался для вас полезным и интересным. С радостью выслушаю ваши вопросы и дам на них ответы.
Приятного Вам творчества!
Всего доброго!
Елена Копченова
Мыльные пузыри – переливающиеся всеми цветами радуги, всегда вызывают улыбку и восторг. А вы знаете, что мыльными пузырями можно рисовать ? Это очень интересная техника, она порадует и взрослых, и детей. Можно не только дуть пузыри , но и делать их цветными, переносить на бумагу.
Что необходимо для работы : вода в баночке, детский шампунь или
жидкое мыло, гуашь,акварель или пищевые красители,плотная бумага, трубочки для коктейля, ложечка.
В воду добавьте шампунь или жидкое мыло. Концентрация примерно 1 :10 (не строго) .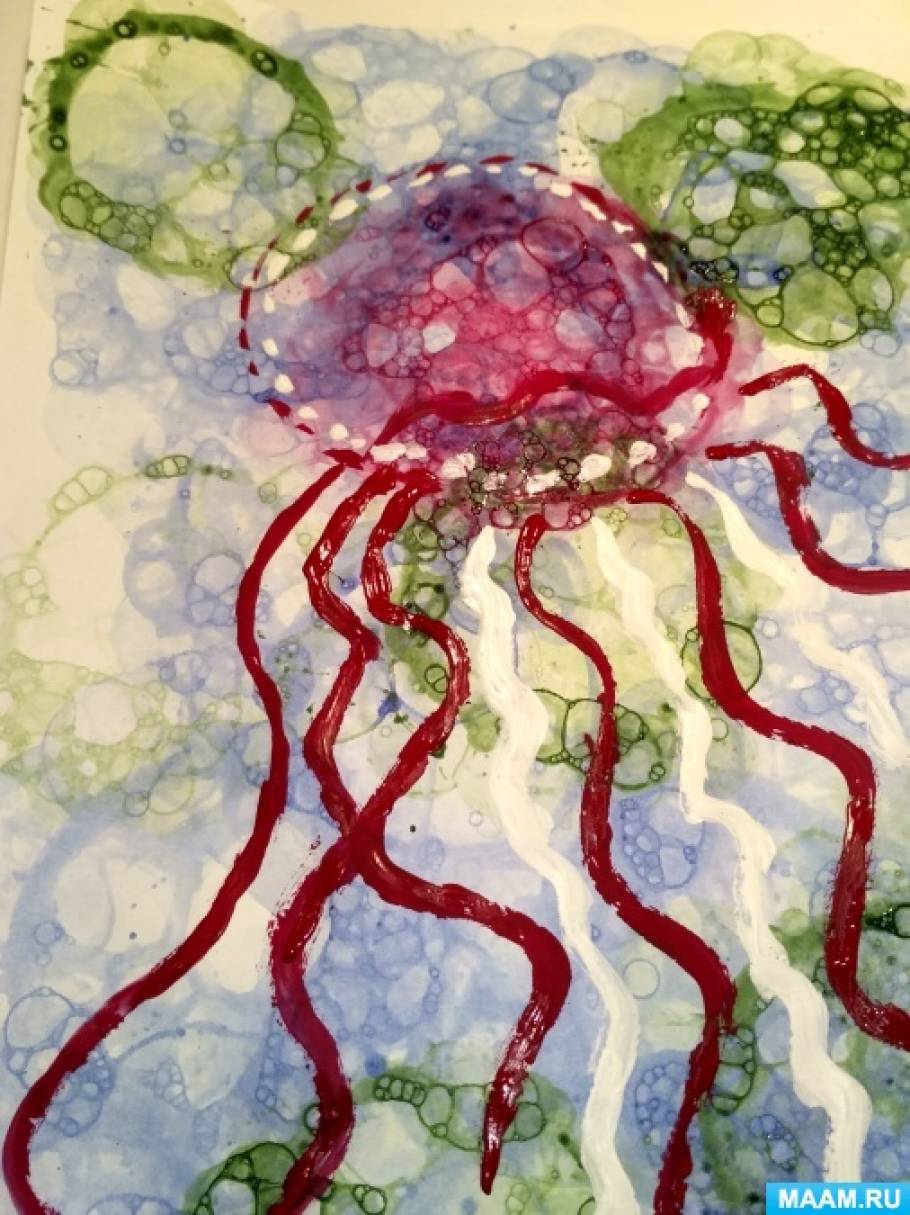 Чтобы пузыри были большими и подолгу не лопались, добавьте в воду чуть-чуть желатина или глицерина. Все ингредиенты перемешайте и оставьте постоять на 2-3 дня. Затем профильтруйте раствор через марлю и оставьте в холодильник на 12 часов. Процедуру можно упростить — просто добавив в воду мыльный раствор и красители .
Чтобы пузыри были большими и подолгу не лопались, добавьте в воду чуть-чуть желатина или глицерина. Все ингредиенты перемешайте и оставьте постоять на 2-3 дня. Затем профильтруйте раствор через марлю и оставьте в холодильник на 12 часов. Процедуру можно упростить — просто добавив в воду мыльный раствор и красители .
Чем больше красителя, тем ярче цвет пузырей .
Все, теперь можно создавать красивые воздушные шары.
1 способ. Берем соломинку для коктейля и начинаем пенить раствор (дуем в трубочку, чтобы пузыри поднялись в баночке . Когда пена поднялась, берем плотную бумагу и прислоняем ее к мыльной пене .
2 способ. Можно снимать поднявшиеся пузыри ложкой и выкладывать на листе.
Таким образом, можно одним листом бумаги пройтись по всем цветам.
А теперь начинаем всматриваться в узоры мыльных пузырей и фантазировать , дорисовывать .
А можно вырезать узор мыльного пузыря и использовать в аппликации.
Используя эти два способа можно получить интересные работы. Судите сами.
Что такое мыльные пузыри, знают абсолютно все. Многие малыши с огромным удовольствием готовят своими руками и придумывают различные способы выдувать из них разноцветные переливающиеся пузырики, а затем гоняют их в помещении и на улице. При определенной сноровке из них можно делать различные фигуры, а также однако это художественное направление знакомо далеко не всем.
В действительности, техника рисования мыльными пузырями необычайно проста и доступна даже для детей дошкольного возраста. Это невероятно веселое, интересное и увлекательное занятие позволяет создавать яркие и оригинальные рисунки, не затрачивая особых усилий, поэтому оно набирает все большую популярность у дошколят и ребят младшего школьного возраста.
В данной статье мы предлагаем вашему вниманию простой мастер-класс, с помощью которого вы освоите рисование мыльными пузырями и своими руками создадите необычную картинку.
Рисуем мыльными пузырями вместе с детьми
Следующая пошаговая инструкция наглядно продемонстрирует вам, как рисовать мыльными пузырями на бумаге:
- Подготовьте необходимые материалы. Вам потребуются мыльные пузыри, акриловая краска, жидкое мыло, а также небольшая пластиковая мисочка и тоненькая трубочка.
- Соедините 1 часть жидкого мыла, такое же количество краски и 2 части дистиллированной воды. Хорошо перемешайте ингредиенты, а затем сделайте множество мелких пузырьков с помощью трубочки.
- Приложите к пузырькам лист бумаги и нажмите довольно сильно, чтобы остался заметный след.
- Повторите все эти действия с краской другого цвета.
- Добиваясь нужной формы, изобразите на листе бумаги вот такие крупные цветы:
- На другом листе бумаги нарисуйте зеленые листики разных оттенков.
- Вырежьте их и аккуратно приклейте их вокруг цветов, чтобы получить красивую картинку.
- Тонкой ручкой черного цвета нарисуйте на листочках прожилки. Ваш рисунок готов!
- Оформить изображение можно и по-другому – просто нарисуйте акварелью несколько тонких стеблей.
- Украсьте их точечками и нарисуйте листики.
- Завершите рисунок таким же образом – начертите тоненькие прожилки ручкой.
У вас получились яркие и оригинальные цветы, нарисованные при помощи мыльных пузырей. Подключив совсем немного фантазии и воображения, вы сможете придумать самые разнообразные картинки и изобразить их на бумаге таким необычным способом.
Статьи по теме:
Мы обязаны нашим дедам за мирное небо, мы всегда помним о их великом подвиге и обязаны доносить это до следующих поколений. Поэтому с приближением 9 мая нужно посвятить пару вечеров ребенку, рассказать о войне и победе, и нарисовать подарок ветерану. |
Нетрадиционные техники и способы рисования для детей: как рисовать мыльными пузырями, мастер-класс.
Рисование мыльными пузырями
Мыльные пузыри — известная детская забава. Хрупкие, прозрачные, они красиво переливаются разными цветами радуги и создают ощущение праздника.
Вот какое стихотворение о них написал Самуил Яковлевич Маршак.
Воды обыкновенной
В стаканчик набери —
Пускать из мыльной пены
Мы будем пузыри.Соломинку простую
Сейчас возьму я в рот,
Воды в нее втяну я,
Потом слегка подую
В соломинку — и вот,Сияя гладкой пленкой,
Растягиваясь вширь,
Выходит нежный, тонкий,
Раскрашенный пузырь.Горит, как хвост павлиний.
Каких цветов в нем нет!
Лиловый, красный, синий,
Зеленый, желтый цвет.Взлетает шар надутый,
Прозрачнее стекла.
Внутри его как будто
Сверкают зеркала.Огнями на просторе
Играет легкий шар.
То в нем синеет море,
То в нем горит пожар.Он, воздухом надутый,
По воздуху плывет,
Но и одной минуты
На свете не живет.Нарядный, разноцветный,
Он лопнул навсегда,
Расплылся незаметно,
Растаял без следа.А был такой надменный,
Заносчивый такой!
Хвалился, что из пены
Родился он морской.В нем столько красок было,
Была такая спесь,
А он — воды и мыла
Раздувшаяся смесь.Его я не жалею…
По правде говоря,
Стихи о нем длиннее
Всей жизни пузыря!
Не все знают о том, что мыльными пузырями можно рисовать. В этом случае они не расплываются незаметно и не тают без следа — след от них превращается в рисунок.
Рисунки в этой необычной технике оказываются такими же необычными, а занятие приносит детям радость. К тому же, отпечатки каждый раз получаются разными, поэтому очень интересно с ними экспериментировать, а потом фантазировать, на что они похожи.
Как рисовать мыльными пузырями. Мастер-класс
Материалы и инструменты
- моющее средство: жидкое мыло, детский шампунь, гель для душа и т.д.
- красители: пищевые (предпочтительнее, потому что в этом случае узоры получаются более тонкими и ажурными) или гуашь
- коктейльные трубочки, ложки
- плотная бумага
Этапы работы
Попробуйте перелить готовый раствор в глубокую тарелку, чашку или миску, чтобы круги-отпечатки получались большими.
2 способ
Еще один способ рисования мыльными пузырями заключается в том, что конец коктейльной трубочки окунают в раствор, надувают мыльный пузырь. Мыльный пузырь не должен улететь, его нужно оставить на трубочке. Затем его очень аккуратно опускают на бумагу, чтобы он на ней лопнул и оставил цветной круглый отпечаток.
Из таких кружочков можно сделать множество самых разных забавных изображений, если дорисовать фломастерами необходимые детали. Например, таким образом можно нарисовать черепашек, жучков, гусеничку, рыбок, букет цветов, рожок с шариками мороженого, связку воздушных шариков и т.д.
Использование бумаги с такими рисунками
Полученную разноцветную бумагу с необычными узорами можно использовать любым из следующих способов:
Предлагаю посмотреть, как мы с дочкой делали и чем они нас удивили или другие мастер-классы по нетрадиционным техникам рисования среди статей с тегом .
© Юлия Валерьевна Шерстюк, https://сайт
Всего доброго! Если статья была вам полезна, пожалуйста, помогите развитию сайта, поделитесь ссылкой на нее в соцсетях.
Размещение материалов сайта (изображений и текста) на других ресурсах без письменного разрешения автора запрещено и преследуется по закону .
Предыдущая статья: «Да здесь всё как будто из-под неволи» Следующая статья: Значение образа кулигина в драме гроза
Рисование мыльными пузырями — изо, презентации
Мыльными пузырями можно не только играть, но и создавать интересные композиции.
Просмотр содержимого документа
«Рисование мыльными пузырями»
Рисование мыльными пузырями.
- Соломинку простую сейчас возьму я в рот, Воды в неё втяну я, потом слегка подую в соломинку – И вот, сияя гладкой плёнкой, растягиваясь вширь, Выходит нежный, тонкий, раскрашенный пузырь.
- Так Самуил Яковлевич Маршак писал о мыльных пузырях.
- Установить точно, когда появились и кто придумал пускать мыльные пузыри невозможно.
- Найденные в Помпеях древние фрески показывают, что уже тогда люди забавлялись этими радужными пузырьками.
- Ещё на картинах фламандских художников 17 века часто встречались изображения детей, выдувающих мыльные пузыри через глиняную соломинку.
- В 18 и 19 веках дети выдували мыльные пузыри, используя мыльную воду, оставшуюся после стирки.
Ж. Б. С. Шарден.
Мыльные пузыри. 1739 г.
Мыльными пузырями и пеной можно рисовать, смешивая с акварелью и гуашью.
Изображения получаются радужными, фантастическими
Проверено, что выдувая мыльные пузыри,
поднимается настроение, забываются все
проблемы, а также хорошо разрабатываются лёгкие.
Всё это благотворно влияет на здоровье.
Материалы для работы:
Вода в смеси
с шампунем (10 к 1)
Краски: акварель, гуашь, тушь
.
Вариантов работы с мыльной пеной несколько. Способ 1.
- Рисование пеной с мелкими пузырями
- Материалы:
- пена для ванн или любое жидкое мыло,
- небольшая миска,
- венчик для взбивания,
- ложка или плоская палочка,
- бумага,
- акварель (жидкая гуашь или акрил).
- Полезный совет или подсказка: Лучший состав для мыльных пузырей: 25 мл глицерина, 150 мл воды и 50 гр. средства для мытья посуды.
Ложкой или палочкой выкладываем сделать карандашны
- В небольшую миску наливаем немного воды (2-3 столовые ложки) и пену для ванн (1-2 столовые ложки).
- Сбиваем все венчиком до образования большого количества пены.
- Ложкой или палочкой выкладываем пену на лист бумаги, следуя форме задуманного рисунка
- (можно заранее сделать карандашный набросок) или создавая произвольное изображение.
- Затем мягкой кистью аккуратно наносим на изображение жидкую акварельную краску, как бы подкрашивая пену .
Даем листу хорошо просохнуть и дорисовываем мыльные пятна до задуманного сюжета .
Способ 2. Рисование пеной с крупными пузырями
- Материалы:
- пена для ванн или любое жидкое мыло,
- небольшие емкости,
- трубочка (соломинка) для коктейлей,
- бумага,
- акварель (жидкая гуашь или акрил).
- смешиваем жидкое мыло или пену для ванн с водой в пропорции примерно один к двум – примерно, потому что пена для ванн и жидкое мыло разных производителей могут пениться по-разному, и надо экспериментировать с тем, что есть именно у вас.
- Добавляем туда акварельную краску или гуашь, подкрашивая растворы до нужной интенсивности цвета или составляем разные оттенки.
- Затем берем трубочку для коктейлей, опускаем ее в раствор и дуем.
- Получается пенистая масса с пузырями разного размера.
- Если пены много, можно приложить к мыльной шапке лист бумаги.
- На листе получится мыльный отпечаток, который можно использовать как фон для рисунка или как фактуру для аппликации.
- При этом способе работы с пеной пузыри будут скорее не яркого цвета, а нежных оттенков.
- Более интенсивных цветов можно добиться, подкрашивая пену кисточкой с краской уже на листе с бумаги, как описано в первом способе.
Дополняем изображение кистью и другими материалами.
Можно дополнить изображение аппликацией.
- Для рисования мыльной пеной лучше подойдет мелованная бумага.
- Она меньше впитывает воду, чем обычная, поэтому фактура высохшей мыльной пены на ней будет проявляться лучше.
- Если мелованной бумаги нет , можно подготовить бумагу самим, заранее покрасив лист водостойкой тушью или акриловыми красками.
- Высохнув, тушь и акриловая краска не будут пропускать воду, но и не окрасят нанесенную сверху мыльную пену.
3 способ. Создание отпечатков от мыльных пузырей.
Для работы потребуется:
Несколько
стаканчиков для
воды.
Цветная тушь или
краски для батика.
Вода.
Жидкое мыло.
Фломастеры.
Трубочки для коктейля.
Лист белой бумаги.
- Приготовить лист.
- Надуть мыльный пузырь и очень аккуратно посадить пузырь на чистый белый лист.
- После того как лист высохнет, берём фломастер или маркер, и начинаем оживлять наш рисунок.
- На одной из цепочек из следов от мыльных пузырей, на первом или последнем круге-отпечатке начинаем рисовать лицо сороконожки, добавляем ей глаза, усики, ротик, носик и так далее.
Ахроматическая композиция с мыльной пеной и тушью
Композиция «Деревья» с доработкой цветными и чёрным фломастером.
- А завершить мастер – класс хотелось бы словами известного писателя Марка Твена:
- « Мыльный пузырь, пожалуй, самое восхитительное и самое изысканное явление природы!»
- Благодарю за внимание!
- Рисование мыльной пеной : Техника для работы с детьми / Д. Герасимова // Искусство. – 2015. – № 10. – С. 46–51.
- http://www.youloveit.ru/creative/uroki_risovaniya/4248-urok-risovaniya-mylnymi-puzyryami.html
Рисуем мыльными пузырями. Домашний рецепт приготовления пузырей. Игры. Мыльные пузыри — легкие, воздушные шарики, переливающиеся всеми цветами радуги, всегда вызывают улыбку и восторг, причем не только у детей, но и у взрослых. У каждого человека, наверное, они ассоциируются с детством. Помните, как весело и интересно лопать мыльные пузырики или просто наблюдать за ними? А вы знали, что можно рисовать мыльными пузырями? О, это самая ошеломляющая техника, любителей мыльных пузырей она очень порадует, ведь теперь можно не только дуть пузыри, но и делать их цветными, переносить на бумагу! Купить мыльные пузыри можно в любом детском магазине. Однако мы предлагаем вам поучаствовать в создании чуда самостоятельно. Итак, как сделать мыльные пузыри? Это совсем не сложно, однако, даже в таком простом деле существуют свои маленькие секреты. Так, например, жесткая вода не годится для изготовления мыльных пузырей. Лучше всего использовать охлажденную кипяченую воду. Рецепт № 1. В воду добавляется шампунь или жидкое мыло. Концентрация примерно 1:10. Пропорция не является строгой, однако резко уходить в сторону все-таки не стоит. Если мыльные пузыри предназначены для маленького ребенка, рекомендуется использовать детский шампунь без слез. Чтобы пузыри были большими и подолгу не лопались, добавьте в воду чуть-чуть желатина или глицерина. Рецепт № 2. (самый простой) 100 гр. средства для мытья посуды 50 мл. глицерина 300 мл. воды Рецепт № 3. 300 мл горячей воды 10 капель нашатырного спирта 150 мл. глицерина 25 гр. моющего средства в виде порошка Все ингредиенты перемешайте и оставьте постоять на 2-3 дня. Затем раствор профильтруйте через марлю и поставьте в холодильник на 12 часов. Все, теперь можно создавать красивые воздушные шары. Рецепт № 4. 50 мл прозрачного геля для душа (можно детского) 60 мл воды 0,5 ч.л. сахара Все перечисленные компоненты нужно соединить, и можно творить чудеса! Рисование мыльными пузырями. Для этого в растворы мыльной воды добавляются краски или пищевой краситель. Берем соломинку для коктейлей и начинаем пенить раствор, чтобы пузыри поднялись в стаканчике. Когда пена поднялась, берем плотную бумагу и прислоняем ее к мыльной пене. Таким образом, можно одним листом бумаги пройтись по всем цветам. Для творчества лучше брать плотную бумагу, а еще лучше бумагу для акварели. 1. 2. 3. 4. 5. 6. Из такой бумаги можно сделать открытки, конверты и… 1. 2. 3. 4. А если рисовать только голубым цветом и потом пририсовать рыбок, то получится океан. А кто сказал, что это только для детей? Игры с мыльными пузырями. Процесс надувания мыльных пузырей очень увлекателен. Однако можно сделать его разнообразным. Можно использовать домашние принадлежности. А чтобы получилось много маленьких мыльных пузыриков, надо их выдувать из нескольких соломинок. Например, можно купить плавающие свечи, налить полную ванну воды, выключить свет и пускать мыльные пузыри. Необыкновенно красивое зрелище! Очень увлекательно надувать пузыри в зимнее время на улице. Интересно, что при температуре -7 °С они могут замерзнуть. Чтобы это произошло, нужно аккуратно положить на пузырь снежинку или опустить его на снег. Чтобы повторить такой фокус, придется потрудиться, однако результат оправдает затраченное время! Можно осуществить и другой трюк. Плоскую тарелку предварительно смочите мыльным раствором. При помощи трубочки надуйте большой пузырь таким образом, чтобы он был на ее поверхности. Затем аккуратненько отсоедините трубочку от стенки пузыря, чтобы она осталась внутри. Надуйте второй пузырь. Если вы сделаете все правильно, получите мыльную «матрешку». А можно «построить» из пузырей такой воздушный замок. Весёлого Творчества! |
Нетрадиционные техники рисования в начальной школе в условиях ФГОС. Мастер-класс «Рисование мыльными пузырями»
Муниципальное общеобразовательное учреждение
основная общеобразовательная школа п. Северный
Хвалынского района Саратовской области
Нетрадиционные техники рисования в начальной школе в условиях ФГОС.
Мастер-класс «Рисование мыльными пузырями»
Выступление в профессиональном конкурсе педагогических работников
«Ярмарка педагогических идей»
Хазитова Ольга Петровна
учитель начальных классов
первая квалификационная категория
2019 г.
Мастер — класс.Тема: «Нетрадиционные техники рисования в начальной школе в условиях введения ФГОС. Рисование мыльными пузырями»
Цель:расширить знания педагогов о нетрадиционных способах рисования, а именно, рисовании мыльными пузырями.
Задачи:
— научить слушателей рисовать мыльными пузырями;
— повысить уровень мастерства педагогов в области нетрадиционного рисования;
— вызвать желание использовать полученные знания в работе.
Методы и приёмы: репродуктивный, практический.
Оборудование: салфетки, материал для практической деятельности – бумага, гуашь разного цвета, стаканы с мыльным раствором разного цвета, трубочки для сока, ложки, стаканы с водой, кисточки,
Предварительная работа: обработка специальной литературы по данной теме; подготовка оборудования; создание компьютерной презентации.
«Истоки способностей и дарования детей – на кончиках их пальцев.
От пальцев, образно говоря, идут тончайшие нити – ручейки, которые питают источник творческой мысли. Другими словами, чем больше мастерства в детской руке, тем умнее ребенок».
В. А. Сухомлинский
Содержание.
— Добрый день, уважаемые коллеги!
— Тема сегодняшнего мастер – класса: «Нетрадиционные техники рисования в начальной школе в условиях введения ФГОС. Рисование мыльными пузырями»
Развитие творческих способностей играет большую роль в развитии коммуникативной компетенции учащихся, их умения нестандартно мыслить, видеть предметы и явления с другой стороны. В концепции федеральных государственных стандартов в качестве конечного результата образовательной деятельности российской школы фиксируется портрет выпускника начальной школы, в котором одно из важнейших мест отводится развитию творческих качеств личности ребёнка. Все мы в детстве были художниками. Каждый ребенок с двух – трех лет и до подросткового возраста рисует грандиозные композиции, рисует вообще все, что слышит и знает, даже запахи.
К 8-10 годам детьми накоплен достаточный жизненный опыт для творчества на новом уровне, так как творческая деятельность зависит от богатства и разнообразия прежнего опыта человека. Этот опыт и есть тот материал, из которого «черпает» идеи фантазия. Развивая воображение детей, мы помогаем им понять, «проиграть» свои устремления, что очень важно для развития внутренней жизни.
Рисование является едва ли не самым интересным видом деятельности детей. Оно позволяет ребенку отразить в изобразительных образах свои впечатления об окружающем, выразить свое отношение к ним. Каждый ребенок по своей природе – творец. Но, как правило, его творческие возможности находятся в скрытом состоянии и не всегда полностью реализуются. Создавая условия, побуждающие ребенка к занятиям искусством, можно раскрыть эти дремлющие до поры до времени творческие наклонности.
Рисование способствует развитию эстетического и эмоционального восприятия искусства, которые в свою очередь способствуют формированию эстетического отношения к действительности. Яркие краски разнообразят жизнь ребенка, восполняют его потребность в приятных ощущениях. Наконец, занятия живописью это одна из форм предметной деятельности ребенка, а предметная деятельность совершенно необходима ребенку для физического, психического и умственного развития.
В современный мир внедряется большое количество инноваций. Это показатель того, что активизировать процесс получения и приобретения знаний можно при использовании новых нетрадиционных средств. Считается, что именно та стратегия учителя наиболее удачна, при которой учебно-познавательная атмосфера создается при использовании новых технологий обучения. Таковыми можно считать творческие задания. В своей работе я часто использую различные методы и приемы рисования нетрадиционными способами.
Нетрадиционное рисование привлекает своей простотой и доступностью, раскрывает возможность использования хорошо знакомых предметов в качестве художественных материалов.
А главное то, что нетрадиционное рисование играет важную роль в общем психическом развитии детей. Ведь главным является не конечный продукт – рисунок, а развитие личности: формирование уверенности в себе, в своих способностях, целенаправленность деятельности.
Нетрадиционные техники позволяют выразить в рисунке чувства и эмоции, дают ребенку свободу и вселяют уверенность в своих силах. Владея разными техниками и способами изображения предметов или окружающего мира, ребенок получает возможность выбора.
Для развития творчества и систематизации знаний детей я поставила перед собой следующие задачи:
Учить детей использовать в рисовании разнообразные материалы и технику, разные способы создания изображения, соединяя в одном рисунке разные материалы с целью получения выразительного образа.
Развивать эстетические чувства формы, цвет, ритм, композицию, творческую активность, желание рисовать. Учить видеть и понимать красоту многоцветного мира.
Формировать у детей творческие способности посредством использования нетрадиционных техник рисования.
Воспитывать умение доводить начатое дело до конца, работать в коллективе, индивидуально.
Нестандартные подходы к организации занятия, вызывают у детей желание рисовать, дети становятся более раскованными, раскрепощенными, уверенными, что их работа лучше всех. У них развивается фантазия, творческое воображение, мышление, любознательность, одаренность, продуктивность, потенциал и интуиция.
Итак, при обучении рисованию могут использоваться самые разнообразные техники и самые разнообразные материалы.
Изобразительная деятельность с применением нетрадиционных материалов и техник способствует развитию у ребёнка:
Мелкой моторики рук и тактильного восприятия;
Пространственной ориентировки на листе бумаги, глазомера и зрительного восприятия;
Внимания и усидчивости;
Мышления;
Изобразительных навыков и умений, наблюдательности, эстетического восприятия, эмоциональной отзывчивости;
Кроме того, в процессе этой деятельности формируются навыки контроля и самоконтроля.
Я предлагаю Вам познакомиться с одним из способов нетрадиционного рисования, рисование мыльными пузырями.
— Для выполнения практической работы предлагаю занять места за этими партами.
— Спасибо, что Вы приняли мое приглашение.
— Одним из интересных приемов является способ рисования мыльными пузырями.
— Мыльные пузыри – переливающиеся всеми цветами радуги, всегда вызывают улыбку и восторг. Это очень интересная техника рисования, она порадует и взрослых, и детей. Можно не только дуть пузыри, но и делать их цветными и переносить на бумагу.
— Для работы нам необходимо: цветной мыльный раствор (гуашь, вода, жидкое мыло – 5:1:1), бумага, стаканчики с водой, гуашь или акварель, кисточки, ложки, салфетки.
— В полиэтиленовые стаканчики, тарелочки положите гуашь, добавьте жидкого мыла, а так же воды. Все это тщательно перемешайте ложкой. По густоте должно получиться, как сливки.
Пропорции: гуашь, мыло, вода — 5:1:1 Краски желательно растворять яркие, от которых следы останутся тоже яркие.
Чем больше красителя, тем ярче цвет пузырей.
Практическая работа педагогов.
— 1-й способ. Опустите в смесь трубочку для сока и подуйте так, чтобы в стакане взбилась цветная пена.
— Возьмите лист бумаги и прислоните его к мыльной пене, накрыв стакан сверху.
— 2-й способ. Можно снимать поднявшиеся пузыри ложкой и выкладывать их на листе
— Таким образом, можно одним листом бумаги пройтись по всем цветам
— А теперь, начинаем всматриваться в узоры мыльных пузырей и фантазировать, дорисовывать кисточкой и гуашью.
Тема: 23 февраля – День Защитника Отечества!
Презентация рисунков на слайдах
Выставка рисунков педагогов
— Как вы считаете это актуально? Полезно? Вам пригодится? У вас появилось желание заняться этим с детьми?
— Перед каждым из Вас на парте лежат по 2 листа: красный и синий. Мне передайте, пожалуйста, только один из них: если Вам понравился сегодняшний мастер — класс — красный, если не понравился — синий.
Разверните лист. (На красных листах напечатаны названия видов работ нетрадиционных способов рисования, синие листы пустые)
— Уважаемые коллеги, спасибо Вам за ваш интерес к моему опыту, активное участие в мастер — классе, за чудесные картины.
— Все мы взрослые родом из детства! Я желаю вам здоровья, счастья, мирного неба над головой и творческих успехов в освоении данного материала.
— Благодарю за сотрудничество! .
Список использованной литературы.
1. Давыдова И.В. Творческая направленность нетрадиционных техник рисования// Начальная школа плюс и после. 2005 №4 с.56
2. Давыдова И.В. Его величество цвет// Школьный психолог. 2008 №1 с.43.
3. Лебедева Л.Д. Арт-терапия детской агрессивности// Начальная школа. 2001 №2. с.24
4.Старикова С. Арт-терапевтические методы в школе// Социальная педагогика. 2008 №1.с.54
Мастер-класс по использованию нетрадиционных методов рисования. Монотипия «Цветы на пене для бритья»
5. Янушко Е.А. Рисование с детьми раннего возраста. – М., 2010.
6. Акуненок Т.С. Использование приемов нетрадиционного рисования. М., – 2010.
7. Шклярова О.В. Рисуйте в нетрадиционной форме . С.-П. – 2013.
8. Юркова Н. Рисование мыльной пеной, крашенными опилками, на самоклеющейся пленке // Обруч. – 2012. — №2 с. 69
9. Лебедева Е.Н. Использование нетрадиционных техник [Электронный ресурс]: http://www.pedlib.ru/Books/6/0297/6_0297-32.shtml
Рисование мыльными пузырями — мастер-класс
Что такое пузыри, знают абсолютно все. Многие малыши с огромным удовольствием готовят себе мыльные растворы и придумывают разные способы выдувать из них разноцветные переливающиеся пузырьки, а затем гонять их в помещении и на улице. При определенном навыке из них можно делать разные формы и рисовать, но это художественное направление знакомо далеко не всем. P>На самом деле техника рисования мыльных пузырей необычайно проста и доступна даже для дошкольников.Это невероятно веселое, интересное и увлекательное занятие позволяет без особых усилий создавать яркие и оригинальные рисунки, поэтому оно приобретает все большую популярность среди дошкольников и молодежи младшего школьного возраста.
В этой статье мы предлагаем вашему вниманию простой мастер-класс, с помощью которого вы освоите рисование мыльными пузырями и создадите свою картину своими руками.
Рисуем пузыри вместе с детьми
Следующая пошаговая инструкция покажет вам, как рисовать пузыри на бумаге:
- Подготовьте необходимые материалы.Вам понадобятся мыльные пузыри, акриловая краска, жидкое мыло, а также небольшая пластиковая миска и тонкая трубочка.
- Смешайте 1 часть жидкого мыла, такое же количество краски и 2 части дистиллированной воды. Хорошо перемешайте ингредиенты, а затем с помощью тюбика сделайте много мелких пузырьков.
- Прикрепите лист бумаги к пузырям и надавите на него с такой силой, чтобы остался видимый след.
- Повторите все эти шаги с краской другого цвета.
- Получив нужную форму, нарисуйте на листе бумаги вот такие большие цветы:
- На другом листе бумаги нарисуйте зеленые листочки разных оттенков.
- Вырежьте их и аккуратно приклейте вокруг цветов, чтобы получился красивый рисунок.
- Тонкой черной ручкой нарисуйте полосы на листьях. Ваш рисунок готов!
- Вы можете нарисовать изображение другим способом — просто нарисуйте тонкие стебли акварелью.
- Украшаем их точками и нарисуем листики.
- Завершите рисунок аналогично — нарисуйте ручкой тонкую прожилку.
У вас получились яркие и оригинальные цветы, нарисованные мыльными пузырями.Соединив совсем немного фантазии и воображения, можно придумать самые разные картинки и таким необычным образом изобразить их на бумаге.
Мастер-класс по рисованию: начните рисовать лучше сегодня
отличные курсы для начинающих
Я научу вас навыкам, необходимым, чтобы выделиться из толпы. Будь то личное увлечение или бизнес, здесь вы можете научиться видео, фотографии, искусству, дизайну, маркетингу и многому другому.
учиться на практике
Пошаговые инструкции и обучение на основе проектов.
получить поддержку
Индивидуальная поддержка от экспертов, которые действительно хотят вам помочь.
не волнуйтесь. повеселись.
С нашей гарантией счастья вам не о чем беспокоиться. Станьте участником или присоединитесь к индивидуальному курсу сегодня. У нас есть 30-дневная гарантия возврата денег на все курсы.
подробнее о phil
Мой профессиональный опыт в производстве и редактировании видео. Я окончила Школу кино и телевидения Университета Лойола Мэримаунт в 2011 году.С тех пор я работал над тысячами проектов, которые появлялись в кинотеатрах, на кинофестивалях, на телевидении и в Интернете.
Сегодня я создаю всевозможные вещи: от фотографий, которые можно увидеть в моем Instagram, до домашнего хлеба на закваске , которым кормит мою семью. Кто знает, куда меня приведет жизнь. Но я знаю, где бы я ни был, я буду творить.
С 2012 года я создаю онлайн-курсы, которые прошли более двух миллионов студентов со всего мира. Темы курсов включают все: от фотографии и видео до курсов по дизайну и бизнесу.Если я не могу этому научить, я сотрудничаю с другими экспертами, которые делятся своими навыками с абсолютными новичками.
Видео школа — это мой веб-сайт, где вы можете пройти мои онлайн-курсы. Вы также можете найти их на лучших платформах курсов, таких как Udemy .
Фотография и друзья — это веб-сайт и сообщество, которые я создал, чтобы помочь новым фотографам стать уверенными в своих камерах.
Не могу дождаться встречи с вами в классе!
— Phil
Мастер-классы по математике для молодежи
Современные «Мастер-классы по математике» в Соединенном Королевстве возникли в 1981 году по инициативе Джорджа Портера, тогдашнего президента Национальной ассоциации одаренных детей.Талант в математике, как и в музыке, можно распознать в раннем возрасте у детей, и поощрение его является общественной услугой, как это сейчас широко принято.
На самом деле идея действительно восходит к Майклу Фарадею, который читал рождественские лекции о науке для молодежи в Королевском институте Великобритании в Лондоне в 1826 году. Сэр Кристофер Зееман, следуя инициативе Портера, прочитал первую серию из шести человек. часовые лекции (мастер-классы по математике) для молодежи в Королевском институте в 1981 году на тему «Природа математики и математика природы».
Следствием этого стали широко распространенные в настоящее время в Соединенном Королевстве инициативы по проведению мастер-классов по математике, особенно для возрастных групп от 8 до 18 лет, и с энтузиазмом местных организаторов. В течение нескольких лет я работал в комитете Королевского института, роль которого заключалась в поощрении проведения этих мастер-классов на национальном уровне.
Разумным определением мастер-класса могло бы быть то, что он разработан для «студентов» (любого возраста), у которых есть готовое любопытство к тому, что происходит вокруг них, и интерес к поиску объяснения того, что они наблюдают, даже если это объяснение не сразу очевидно, но требует, возможно, двух- или трехэтапного процесса для достижения решения.«Оратор» будет искренне заинтересован в получении ответа от таких студентов, а также в разработке задач из любых обстоятельств, лежащих в пределах только что указанной области. В математике процесс решения обычно требует идентификации подходящих «переменных» для описания проблемы, формулировки подходящих соотношений (уравнений) между этими переменными, а затем «решения» этих уравнений способом, который выражает неизвестную величину. полностью в известных количествах.Так «работает» математика.
Каждый год в 1990-х годах в Беркшире, Англия, шестьдесят 12-летних учеников собирались на мастер-классы по математике в Университете Рединга. Участники были номинированы школами и продемонстрировали способности к математике. Были проведены две параллельные сессии, в каждой из которых участвовало 30 учеников, преподаватель и квалифицированные помощники.
День числа Пи 2009, созданный Северной библиотекой CCAC. CC BY 2.0 через Flickr.Типичный мастер-класс может длиться до трех часов (с перерывами на отдых и учебными занятиями с перемежением лекционных материалов) и разбит на три занятия.В идеале должно быть несколько учителей-добровольцев, которые будут давать советы во время учебных занятий. Учителя из участвующих школ с готовностью проявили энтузиазм, чтобы добровольно выступить в этой роли.
Примеры тем, рассматриваемых на мастер-классах: «Погода» (атмосфера и силы в ней) сэра Брайана Хоскинса, «Волны на воде» (на глубокой и мелкой воде, группами) Уинифред Вуд и «Динамика динозавров» (например, их вес и скорость) Майкла Сьюэлла.Я также провел мастер-класс по теме «Воздушные шары и пузыри», в котором использовалась математика, связанная с демонстрациями в классе, чтобы проиллюстрировать связанную последовательность тем: давление, равновесие сферического пузыря, натяжение мыльной пленки, натяжение резины, пики давления и ямки, и цилиндрические шары.
Долгосрочная выгода от мастер-класса и одна из его целей состоит в том, чтобы стимулировать постоянный энтузиазм и любопытство по поводу того, как создать «модель» природного явления с помощью математики, и тем самым развить способность к оригинальному мышлению. наблюдаемая ситуация в природе, и которая до сих пор остается в поле зрения школьников.
Примером повседневной проблемы, подходящей для мастер-класса, является следующая «Проблема кафе», фактически поставленная мне моей женой в той ситуации. Учитывая восемь точек, равномерно распределенных по кругу, сколько треугольников разной формы можно нарисовать, используя только три из этих точек в качестве вершин? Теперь обобщите проблему, введя более равномерно расположенные точки и ища разные многоугольники (а не только треугольники). Это учит, как осознать, что любая данная проблема может быть началом гораздо более крупной проблемы, которая является важной частью любого математического исследования и которая может быть не очевидна с первого взгляда.
Еще один пример проблемы мастер-класса: Нарисуйте прямоугольный треугольник с неравными короткими сторонами. Нарисуйте три круга, диаметр каждой из которых будет использоваться в качестве диаметра. Две внешние области между большим кругом и (в свою очередь) двумя меньшими кругами называются лунками (потому что каждая из них имеет форму полумесяца). Теперь докажите теорему Гиппократа (ок. 410 г. до н. Э.) О том, что сумма площадей внешних лунок равна площади прямоугольного треугольника.
Featured image: Calculator by 422737. Public domain via Pixabay .
Мёбиус-инвариантная диаграмма мощности и ее приложения к мыльным пузырям и планарному чертежу Ломбарди
Как мы показываем в этом разделе, нашу инвариантную Мёбиус диаграмму мощности можно использовать для построения плоских кластеров мыльных пузырей с любой реализуемой топологией, приводящей к графу -теоретическая характеристика этих кластеров.
Математическая модель мыльных пузырей
Два классических результата описывают геометрию мыльных пузырей. Законы Плато , экспериментально наблюдаемые в 19 веке Джозефом Плато [45] и строго доказанные для минимальных поверхностей в 1976 году Джином Тейлором [54], утверждают, что в трехмерном кластере мыльных пузырей
Каждая двумерная поверхность имеет постоянную среднюю кривизну . То есть две основные кривизны поверхности принимают одно и то же среднее значение во всех точках поверхности.
На каждом одномерном стыке поверхностей встречаются ровно три поверхности, которые образуют двугранные углы \ (2 \ pi / 3 \) друг с другом.{-1} (- 1/3) \) друг с другом (тот же угол, который образуется лучами из центра правильного тетраэдра через его вершины).
Уравнение Юнга – Лапласа , также сформулированное в XIX веке Томасом Янгом и Пьером-Симоном Лапласом, утверждает, что средняя кривизна двумерной поверхности в кластере мыльных пузырей пропорциональна разнице давления на две стороны поверхности с константой пропорциональности, определяемой поверхностным натяжением жидкости, образующей мыльные пузыри [36].
В случае кластера мыльных пузырей, образованного между двумя плоскими пластинами, стенки пузыря перпендикулярны пластинам, и все поперечные сечения пузырей плоскостью, параллельной одной из пластин, совпадают друг с другом. В этом случае основная кривизна в направлении, перпендикулярном пластинам, равна нулю, и мы можем упростить оба закона, чтобы описать плоскую фигуру, образованную поперечными сечениями.
Таким образом, двумерное ограничение законов Плато гласит:
Фигура состоит из одномерных кривых постоянной кривизны; то есть дуги окружности или отрезки линий, которые не пересекают друг друга.
В каждой конечной точке одной из этих дуг или сегментов пересекаются ровно три кривые, которые образуют друг с другом углы \ (2 \ pi / 3 \).
Соответственно, двумерное ограничение уравнения Юнга – Лапласа утверждает, что:
Кривизна любой из дуг окружности (обратная ее радиусу) пропорциональна разнице давлений между пузырями, которые она разделяет.Пузырьки с одинаковым давлением разделены отрезками прямой с нулевой кривизной.
Мы определяем плоский кластер мыльных пузырей как конечный набор кривых, подчиняющихся планарным ограничениям законов Плато и уравнению Юнга – Лапласа (для некоторого назначения давления каждому пузырю). Эквивалентно, в терминологии теории графов, это планарное вложение графа с ребрами дуги окружности, образующими углы \ (2 \ pi / 3 \) в каждой вершине, для которых можно найти задание давления на пузыри, которые соответствуют всем кривизнам дуги.Как мы описываем в разд. 5.2, мы можем заменить это экзистенциальное условие (существование согласованного задания давления) более простым утверждением о кривизне троек дуг, пересекающихся в вершинах. В плоском кластере мыльных пузырей локальные силы на каждой вершине или дуге, вызванные давлением и поверхностным натяжением, будут в сумме равны нулю, поэтому он будет находиться в состоянии равновесия (хотя, возможно, и нестабильного [23, 58]).
Как позже покажут наши результаты, рисунки Ломбарди, изображенные на рис. 6 и 8 (без вершинных дисков) образуют примеры кластеров мыльных пузырей.Напротив, на рис. 16 изображен плоский 3-регулярный рисунок Ломбарди, который не является кластером мыльных пузырей, потому что он не подчиняется уравнению Юнга – Лапласа. На этом рисунке нет давления на пузырьки, которое согласуется с кривизной их дуг, а в шести асимметричных вершинах на рисунке кривизны трех падающих дуг не равны нулю, что нарушает локальную переформулировку уравнение Юнга – Лапласа, описанное в разд. 5.2.
Рис. 16Набор сегментов и дуг, который подчиняется законам Плато, но не образует плоский кластер мыльных пузырей, поскольку у него нет действительного назначения давления, согласующегося с его кривизной дуги.Три его сегмента не разделяют разные области, что невозможно для мыльных пузырей
Локализация уравнения Юнга – Лапласа
Удобно заменить уравнение Юнга – Лапласа более локальным критерием, используя вариацию кривизны со знаком. Для данной дуги окружности, заканчивающейся в точке \ (p \), кривизны \ (c \ ge 0 \), мы определяем кривизну со знаком дуги в \ (p \) как \ (c \) всякий раз, когда дуга изгибается по часовой стрелке, когда она выходит из \ (p \), и должна быть \ (- c \), когда она изгибается против часовой стрелки.Для линейных сегментов, конечно, кривизна со знаком равна нулю.
Лемма 8Конечный набор дуг окружностей и сегментов линий формирует плоский кластер мыльных пузырей тогда и только тогда, когда он подчиняется законам Плато и в каждой конечной точке дуги или сегмента сумма кривизны со знаком трех входящих кривых равна нулю.
ПробаПусть в одном направлении в плоском кластере мыльных пузырей \ (x \), \ (y \) и \ (z \) будут давления трех пузырей, которые встречаются в одной точке.По предположению, кластер подчиняется уравнению Юнга – Лапласа, согласно которому три знаковые кривизны дуг в точке пропорциональны разностям давления \ (x-y \), \ (y-z \) и \ (z-x \). Тот факт, что эти три кривизны со знаком равны нулю, следует из простого алгебраического факта, что \ ((x-y) + (y-z) + (z-x) = 0 \).
В другом направлении, предположим, что конечное число дуг окружности подчиняется законам Плато и имеет знаковые кривизны, добавляемые к нулю в каждой точке пересечения трех дуг.Мы должны приписать давления пузырькам, образованным дугами, таким образом, чтобы кривизна подчинялась уравнению Юнга – Лапласа. Назначьте нулевое давление для внешней области. Для каждого ограниченного пузыря \ (B \) произвольно выберите кривую \ (c \), которая начинается во внешней области, заканчивается внутри \ (B \), пересекает дуги только в точках надлежащего пересечения внутри дуги и имеет конечное много пунктов пропуска. Установите давление в пределах \ (B \) как сумму разностей давлений, определяемых кривизной каждой пересекаемой дуги.
Чтобы показать, что эта система давлений подчиняется уравнению Юнга – Лапласа, рассмотрим любые два пузыря \ (B_1 \) и \ (B_2 \), разделенные дугой \ (A \), и пусть \ (c_1 \) и \ ( c_2 \) — кривые от внешней области до \ (B_1 \) и \ (B_2 \), по которым определялись их давления. Мы можем связать \ (c_1 \) и \ (c_2 \) другой кривой, которая полностью остается внутри внешней области, образуя единую (возможно, самопересекающуюся) кривую, соединяющую \ (B_1 \) с \ (B_2 \), и мы можем непрерывно деформировать эту кривую, пересекая, как и мы, конечное число тройных точек системы дуг, пока она не образует отрезок прямой, пересекающий дугу \ (A \).Каждый раз, когда эта деформация заставляет кривую пересекать тройную точку, предположение, что кривизна в этой точке складывается с нулем, гарантирует, что сумма разностей давлений на пересечениях вдоль кривой останется постоянной. До деформации эта сумма представляла собой разность давлений между \ (B_1 \) и \ (B_2 \) в нашей системе давлений, а после деформации — разность давлений, требуемая между пузырьками \ (B_1 \) и \ (B_2 \), чтобы кривизна \ (A \) подчинялась уравнению Юнга – Лапласа.Поскольку эти две разности давления равны, \ (A \) (и по тому же аргументу каждая дуга) подчиняется уравнению. \(\квадратный \)
Аналогичный результат для пузырей на сфере вместо плоскости содержится в приложении Куинна Мормана к [47].
Когда три трехмерных пузыря образуют кластер, в котором все участки поверхности имеют сферическую форму, Плато было известно, что три участка внутренней поверхности имеют центры кривизны, которые все лежат на одной линии [31].Хотя центры окружностей и коллинеарность точек не являются свойствами, инвариантными по Мёбиусу, мы можем переформулировать то же свойство коллинеарности для кластеров плоских пузырей с инвариантностью Мёбиуса в терминах точек пересечения окружностей. Это переформулировка позволит нам доказать, что преобразование Мёбиуса плоского кластера мыльных пузырей само по себе является еще одним плоским кластером мыльных пузырей.
Лемма 9Пусть три дуги окружности пересекаются под углами \ (2 \ pi / 3 \) в точке \ (X \) с центрами кривизны \ (C_i \) для \ (i \ in \ {1,2,3 \ } \), и пусть \ (r_i = | XC_i | \) — радиусы каждой из трех дуг.Тогда следующие три условия эквивалентны:
- 1.
Сумма трех кривизны дуг со знаком равна нулю.
- 2.
Три центральные точки \ (C_i \) коллинеарны.
- 3.
Три окружности с центрами \ (C_i \) и радиусами \ (r_i \) имеют две тройные точки пересечения.
Разобьем доказательство на четыре импликации между тремя условиями леммы.
\ ((1) \ Rightarrow (2) \): Предположим, что сумма трех искривлений со знаком равна нулю; тогда у одного должен быть другой знак, чем у двух других.Без ограничения общности (путем перестановки индексов и зеркального отображения конфигурации, если необходимо) мы можем предположить, что знаковые кривизны равны \ (1 / r_1 \), \ (- 1 / r_2 \) и \ (1 / r_3 \ ). По предположению, сумма этих трех величин равна нулю; умножая каждый член этой суммы на \ (r_1r_2r_3 \) и переставляя, мы получаем уравнение \ (r_1r_2 + r_2r_3 = r_1r_3 \).
Обратите внимание, что три линии \ (XC_i \) образуют углы \ (\ pi / 3 \) друг с другом, потому что они перпендикулярны дугам, которые встречаются под углами \ (2 \ pi / 3 \).Предположение о знаках кривизны означает, что углы \ (C_1XC_2 \) и \ (C_2XC_3 \) должны быть равны \ (\ pi / 3 \), а угол \ (C_1XC_3 \) должен быть равен \ (2 \ pi / 3 \). Теперь рассмотрим площади трех треугольников \ (C_1XC_2 \), \ (C_2XC_3 \) и \ (C_1XC_3 \). В любом треугольнике площадь может быть вычислена по формуле сторона-угол-сторона как половина произведения двух смежных длин сторон на синус угла, образованного теми же двумя сторонами. Таким образом, эти области треугольника равны \ (\ frac {1} {2} r_1r_2 \ sin \ frac {\ pi} {3} \), \ (\ frac {1} {2} r_2r_3 \ sin \ frac {\ pi} {3} \) и \ (\ frac {1} {2} r_1r_3 \ sin \ frac {2 \ pi} {3} \) соответственно.Но \ (\ sin \ pi / 3 = \ sin 2 \ pi / 3 \), поэтому из уже полученного уравнения \ (r_1r_2 + r_2r_3 = r_1r_3 \) следует, что треугольники \ (C_1XC_2 \) и \ (C_2XC_3 \) вместе имеют ту же общую площадь, что и треугольник \ (C_1XC_3 \). Это могло произойти только в том случае, если три центра \ (C_1 \), \ (C_2 \) и \ (C_3 \) лежат на одной прямой, иначе сумма площадей \ (C_1XC_2 \) и \ (C_2XC_3 \) будет отличаться от площади \ (C_1XC_3 \) на площадь треугольника \ (C_1C_2C_3 \), которая равна нулю только тогда, когда эти три точки лежат на одной прямой.
\ ((2) \ Rightarrow (1) \): По (2) три центральные точки \ (C_i \) коллинеарны; без ограничения общности предположим, что \ (C_2 \) лежит между \ (C_1 \) и \ (C_3 \) на их общей прямой.Поскольку три центра \ (C_1 \), \ (C_2 \) и \ (C_3 \) образуют углы \ (\ pi / 3 \), а не \ (2 \ pi / 3 \), кривизна со знаком средний центр \ (C_2 \) имеет знак, противоположный знаковой кривизне трех других кривизны; мы можем предположить без ограничения общности (путем зеркального изменения конфигурации, если необходимо), что эти три кривизны со знаком являются \ (1 / r_1 \), \ (- 1 / r_2 \) и \ (1 / r_3 \). Как и в предыдущем случае, три линии \ (XC_i \) образуют углы \ (\ pi / 3 \) друг с другом, поэтому углы \ (C_1XC_2 \) и \ (C_2XC_3 \) должны быть равны \ (\ pi / 3 \), угол \ (C_1XC_3 \) должен быть равен \ (2 \ pi / 3 \), и по коллинеарности два треугольника \ (C_1XC_2 \) и \ (C_2XC_3 \) вместе непересекаются, покрывая ту же область плоскости, что и один треугольник \ (C_1XC_3 \).
Мы можем применить формулу стороны-угла-стороны к этой области двумя разными способами, получив уравнение
$$ \ begin {align} \ frac {1} {2} r_1r_2 \ sin \ frac {\ pi} {3 } + \ frac {1} {2} r_2r_3 \ sin \ frac {\ pi} {3} = \ frac {1} {2} r_1r_3 \ sin \ frac {2 \ pi} {3}. \ end {align} $$
Но множители \ (1/2 \) сокращаются, как и множители \ (\ sin \ pi / 3 = \ sin 2 \ pi / 3 \), оставляя более простое уравнение \ (r_1r_2 + r_2r_3 = r_1r_3 \). Разделение всех членов на \ (r_1r_2r_3 \) дает \ (1 / r_3 + 1 / r_1 = 1 / r_2 \), а перестановка дает \ (1 / r_1-1 / r_2 + 1 / r_3 = 0 \) по желанию.
\ ((2) \ Rightarrow (3) \): три круга имеют по крайней мере одну тройную точку пересечения в \ (X \). Пусть \ (\ ell \) — линия, проходящая через три центра, существующая согласно (2). Тогда, поскольку \ (\ ell \) проходит через центр каждого круга, отражение в \ (\ ell \) является симметрией каждого круга и, следовательно, всей конфигурации трех кругов. Точка \ (X \) не может лежать на \ (\ ell \), потому что две окружности с центром на прямой не могут пересекаться в точке, которая также находится на прямой, они могут встретиться только в точке касания, что нарушает предположение, что дуги пересекаются под углами \ (2 \ pi / 3 \).Следовательно, отражение \ (X \) относительно \ (\ ell \) также является точкой тройного пересечения, и три окружности имеют два тройных пересечения в качестве (3) состояний.
(3) \ (\ Rightarrow (2) \): Для любых двух пересекающихся окружностей обязательно верно, что их центры лежат на серединном перпендикуляре хорды, соединяющей их две точки пересечения. Но по предположению (3), что есть две тройные точки пересечения, хорды, определяемые каждой парой из трех данных окружностей, совпадают; следовательно, их серединные перпендикуляры также совпадают на прямой \ (\ ell \), которая содержит центры всех трех окружностей.\(\квадратный \)
На рис. 17 показан набор дуг, окружностей, центров и радиусов, удовлетворяющих условиям леммы. Лемма применяется непосредственно только к дугам окружности, а не к отрезкам прямых; для сегментов линии нам нужно более осторожное заявление.
Рис.17Дуги, удовлетворяющие условиям леммы 9
Лемма 10Пусть три дуги окружности или отрезки прямой пересекаются под углами \ (2 \ pi / 3 \) в точке \ (X \).Тогда следующие два условия эквивалентны:
- 1.
Сумма трех кривизны дуг и сегментов со знаком равна нулю.
- 2.
Три окружности или прямые, содержащие три дуги или отрезки прямых, имеют две тройные точки пересечения (возможно, включая бесконечно удаленную точку).
Мы рассматриваем разные случаи для каждого возможного количества отрезков прямых во входной конфигурации.
Когда нет отрезков и трех дуг окружностей, лемма представляет собой упрощенную формулировку леммы 9.
Когда есть один линейный сегмент и две дуги окружности, сумма кривизны равна нулю тогда и только тогда, когда две дуги являются отражениями друг друга через линейный сегмент (в противном случае их две кривизны не могут компенсироваться) и есть вторая тройная точка пересечения, если и только если выполняется одно и то же условие отражения (в противном случае два круга пересекут линию в разных точках).
Когда есть два отрезка и одна дуга окружности, сумма кривизны всегда отлична от нуля (она равна кривизне дуги окружности), и имеется только одна тройная точка пересечения (две линии имеют второе пересечение на бесконечности и их пересечения с окружностью в конечных точках).
Когда есть три отрезка линии, сумма кривизны всегда равна нулю, так как все кривизны сами равны нулю, и три прямые пересекаются в точке \ (X \) и в точке на бесконечности, поэтому оба условия выполняются.
Поскольку эквивалентность сохраняется во всех возможных случаях, в общем случае она выполняется. \(\квадратный \)
Это свойство тройного пересечения тесно связано с леммой 5.1 из [60], а также с существованием и единственностью стандартного двойного пузыря, о котором см., Например, Предложение 14.1 из [44].
Инвариантность Мебиуса
Преобразования Мебиуса не сохраняют физически значимые количества мыльных пузырей, такие как их давление, общая длина или площадь мыльной пленки.Они даже не сохраняют конечность пузырей: можно найти преобразование, которое переводит неограниченную область плоскости в ограниченную область и наоборот. Тем не менее, как ни странно, они превращают скопления мыльных пузырей в другие скопления мыльных пузырей. Ниже мы намечаем доказательство инвариантности Мёбиуса.
Лемма 11Пусть \ (B \) — плоский кластер мыльных пузырей, и пусть \ (\ mu \) — преобразование Мёбиуса, обладающее тем свойством, что никакая кривая или дуга \ (B \) не превращается в луч или двойной луч.Тогда \ (\ mu (B) \) также является плоским кластером мыльных пузырей.
ПробаПо леммам 8 и 10, \ (B \) состоит из дуг или отрезков, пересекающихся под углами \ (2 \ pi / 3 \), так что каждые три пересекающиеся дуги имеют окружности, образующие два тройных пересечения. Углы встречи и тройные пересечения окружностей сохраняются преобразованием Мёбиуса, поэтому \ (\ mu (B) \) также является набором дуг или сегментов, пересекающихся под углами \ (2 \ pi / 3 \), так что каждые три пересекающиеся дуги имеют окружности, образующие два тройных пересечения.Снова по лемме 10 кривизны со знаком в каждой точке пересечения \ (\ mu (B) \) складываются в ноль, и снова по лемме 8 \ (\ mu (B) \) является плоским кластером мыльных пузырей. \(\квадратный \)
Отсутствие мостов
На основе мебиусовской инвариантности плоских кластеров мыльных пузырей в этом разделе мы доказываем необходимость нашей теоретико-графической характеристики: каждый плоский кластер мыльных пузырей происходит из графа, который является плоским, 3-регулярным и 2-связным. .
Ясно, что плоский кластер мыльных пузырей должен образовывать планарный граф, а законы Плато подразумевают, что он должен быть 3-регулярным, поэтому нетривиальной частью нашей характеристики графов мыльных пузырей является утверждение, что эти графы являются 2-вершинными. -связны, или, что то же самое (поскольку они трехрегулярны), у них нет мостов.На языке мыльных пузырей это означает, что каждая дуга или сегмент в кластере разделяет два разных пузыря. Как мы сейчас доказываем, это обязательно верно для плоского кластера мыльных пузырей.
Лемма 12В плоском кластере мыльных пузырей ни один сегмент или дуга не могут иметь одинаковые пузыри на обеих сторонах.
ПробаДопустим от противного, что кластер включает в себя сегмент или дугу \ (e \), имеющую одинаковые пузыри с обеих сторон.Ненулевая кривизна \ (e \) противоречила бы уравнению Юнга – Лапласа, поскольку давление одинаково по обе стороны от \ (e \). Но если \ (e \) — отрезок прямой, то легко найти преобразование Мёбиуса, которое преобразует \ (e \) в кривую дугу. Полученный кластер снова противоречит уравнению Юнга – Лапласа, а по лемме 11 непреобразованный кластер также противоречит тому же уравнению. \(\квадратный \)
Реализация графов как мыльных пузырей
Как мы теперь показываем, шаги нашего алгоритма рисования Ломбарди, которые применяются к 2-связным или 3-связным графам, генерируют кластеры мыльных пузырей, давая нам алгоритмическое доказательство того, что наши необходимые условия для графа графика скопления мыльных пузырей также достаточно.
Лемма 13Пусть \ (\ mathcal {D} \) набор из трех касательных друг к другу окружностей. Тогда их мебиус-инвариантная степенная диаграмма \ (M (\ mathcal {D}) \) представляет собой двойной пузырь, образованный тремя дугами окружностей, отрезками прямых или лучами, пересекающимися в двух тройных точках пересечения под углами \ (2 \ pi / 3 \) со знаковой кривизной, равной нулю.
ПробаПо лемме 3 \ (M (\ mathcal {D}) \) есть изображение при преобразовании Мёбиуса трех лучей, пересекающихся под углами \ (2 \ pi / 3 \).Эти лучи встречаются в двух тройных точках пересечения, общей вершине лучей и бесконечно удаленной точке, и это свойство тройного пересечения сохраняется при преобразовании Мёбиуса. Утверждение, что сумма кривизны преобразованных лучей равна нулю, следует из леммы 10. \ (\ square \)
Теорема 5Мультиграф \ (G \) может быть реализован как дуги и стыки плоского кластера мыльных пузырей тогда и только тогда, когда \ (G \) плоский, 3-регулярный и без мостов.
ПробаПланарность и 3-регулярность следуют из законов Плато. Требование того, чтобы плоский кластер мыльных пузырей был без мостов, является леммой 12. Осталось показать, что любой плоский, 3-регулярный граф без мостов \ (G \) может быть реализован как мыльный пузырь.
Если \ (G \) плоская, 3-регулярная и 3-связная, то (как в разделе 4.1) \ (G \) может быть изображена как инвариантная Мёбиус диаграмма степеней \ (M (\ mathcal {D }) \) для упаковки кругов \ (\ mathcal {D} \), представляющей двойственный граф к \ (G \).В каждой вершине диаграммы пересекаются области трех касательных друг к другу окружностей \ (\ mathcal {D} \). По лемме 13 вершина инцидентна трем дугам окружности, пересекающимся под углами \ (2 \ pi / 3 \) (удовлетворяющим законам Плато), причем кривизны со знаком в сумме равны нулю. Следовательно, по лемме 8 диаграмма образует плоский кластер мыльных пузырей, представляющий \ (G \).
Наконец, если \ (G \) безмостовой, плоский и 3-регулярный, но не 3-связный, он должен быть 2-связным. В этом случае, как в разд.4.2 и рис. 9, он может быть сформирован путем построения SPQR-дерева, представляющего 3-связные компоненты \ (G \), отдельно рисуя каждую 3-связную компоненту в виде двойного пузыря или инвариантной Мёбиуса степенной диаграммы круга. упаковка, преобразование этих чертежей так, чтобы они не пересекались друг с другом и чтобы виртуальные ребра, которые соединяются с каждым узлом S, лежали на общем круге, удаление виртуальных ребер и рисование реальных ребер узла S вдоль общего круга. Как и в трехсвязном случае, рисунок каждого компонента подчиняется законам Плато и имеет нулевую сумму кривизны в каждой вершине.По лемме 11 эти свойства сохраняются на этапе алгоритма рисования, который преобразует каждый компонент. Шаг алгоритма, который удаляет виртуальные ребра и заменяет их реальными ребрами, не изменяет локальную геометрию в любой вершине чертежа, поэтому снова сохраняет свойства подчинения законам Плато и нулевой суммы локальной кривизны. Таким образом, после этих шагов у нас есть рисунок, который продолжает подчиняться этим свойствам. По лемме 8 диаграмма образует плоский кластер мыльных пузырей, представляющий \ (G \).\(\квадратный \)
Отметим, что, хотя наш метод упаковки кругов способен реализовать все графы плоских кластеров мыльных пузырей, он не способен генерировать все допустимые геометрии плоских кластеров мыльных пузырей. В частности, в трехсвязном случае создаваемые нами кластеры обладают тем свойством, что внутри каждого пузыря есть окружность, касательная ко всем дугам пузыря, но это свойство не выполняется для произвольных кластеров мыльных пузырей. Например, не все пузыри на рис.У меня есть это свойство.
Стабильность
До сих пор мы рассматривали только то, находится ли пузырьковый кластер в равновесии или нет, но мы можем дифференцировать, в каком равновесии находится кластер, по его стабильности, описывая связь между энергией равновесия и энергией равновесия. энергия соседних конфигураций. Для этого нам потребуются дополнительные определения. В случае пузырьковых кластеров мы можем определить конфигурацию как семейство локально-гладких кривых, которые разделяют пространство на фиксированное количество областей (где каждая область не обязательно может быть соединена).Окрестность данной конфигурации \ (B \) — это набор всех конфигураций, для которых расстояние Хаусдорфа каждой области до соответствующей области \ (B \) находится в пределах некоторого порога.
Есть два естественных способа определения энергии конфигурации. Если каждый пузырек в кластере содержит фиксированное количество сжимаемого газа, то энергия, естественно, может быть определена как сумма двух членов, один для натяжения стенок пузыря, а другой для давления внутри пузырей.То есть энергия равна \ (\ gamma L + \ sum P_i A_i \), где \ (A_i \) — площадь \ (i \) -го пузыря, \ (P_i \) — разность его давления (смоделировано согласно закону идеального газа) от окружающей среды, \ (L \) — общая длина кривых в кластере, а \ (\ gamma \) — поверхностное натяжение, константа пропорциональности уравнения Юнга – Лапласа. В качестве альтернативы, мы можем ограничить окрестности конфигурации, чтобы поддерживать фиксированную площадь для каждого пузыря, и использовать только первый член \ (\ gamma L \) для энергии; это описывает предельный случай, в котором каждый пузырек содержит фиксированное количество несжимаемой жидкости.
С этими определениями окрестностей и энергии устойчивое равновесие — это пузырьковый кластер, который однозначно достигает минимальной энергии. Метастабильное равновесие — это пузырьковый кластер, который не является стабильным, но имеет окрестности, в пределах которых он однозначно достигает минимальной энергии. Неустойчивое равновесие представляет собой пузырьковый кластер, все окрестности которого содержат кластер с более низкой энергией. А нейтральное равновесие — это пузырьковый кластер, который не является ни метастабильным, ни нестабильным: каждая окрестность содержит другой кластер с равной или более низкой энергией, но существует окрестность, которая не содержит никаких состояний с более низкой энергией.
Когда разрешены все четыре вида равновесия, теорема 5 характеризует графики равновесных пузырьковых кластеров. Однако запрет на нестабильное и нейтральное равновесие меняет эту характеристику, как мы сейчас показываем. Для этого мы снова используем инвариантность Мёбиуса, чтобы доказать, что не-3-связные кластеры обязательно включают кокциркулярные особенности, несовместимые со стабильностью.
Лемма 14Пусть \ (G \) будет графом плоского кластера мыльных пузырей \ (B \), имеющего два ребра \ (e_1 \) и \ (e_2 \), такие что \ (G {\ setminus} \ {e_1, e_2 \} \) отключен.Тогда в \ (B \), \ (e_1 \) и \ (e_2 \) образуют кокружные дуги или коллинеарные отрезки.
ПробаПредположим от противного, что \ (e_1 \) и \ (e_2 \) лежат на разных окружностях или прямых. Тогда мы могли бы найти точку \ (q \), которая лежит на окружности или прямой, содержащей \ (e_1 \) (но не принадлежит самому \ (e_1 \)), не пересекается с окружностью или прямой, содержащей \ (e_2 \), а также не пересекается со всеми остальными дугами \ (B \).По лемме 11 преобразование Мёбиуса \ (\ mu \), определенное инверсией через \ (q \), превратит \ (B \) в другой пузырьковый кластер \ (\ mu (B) \), в котором \ (\ mu ( e_1) \) становится отрезком линии, а \ (\ mu (e_2) \) остается изогнутым. Но это противоречит уравнению Юнга – Лапласа, потому что обе дуги должны разделять одни и те же два пузыря и, следовательно, должны иметь одинаковую кривизну. Это противоречие показывает, что \ (e_1 \) и \ (e_2 \) кокциркулярны. \(\квадратный \)
Теорема 6Пусть \ (G \) — несвязный плоский граф.Тогда \ (G \) не может быть графиком стабильного или метастабильного пузырькового кластера, независимо от того, измеряется ли энергия как \ (\ gamma L \) или \ (\ gamma L + \ sum P_i A_i \).
ПробаМы можем предположить, что \ (G \) 3-регулярный и без мостов, иначе это не будет графом пузырькового кластера независимо от устойчивости. Пусть \ (B \) — пузырьковый кластер, представляющий \ (G \). Дерево SPQR \ (G \) включает S-узел с ребрами, которые чередуются между реальными и виртуальными (лемма 5).Удаление любых двух его реальных ребер \ (e_1 \) и \ (e_2 \) разбило бы граф на две отдельные компоненты, поэтому по лемме 14 эти два ребра должны быть представлены в \ (B \) дугами одного и того же круг. Из-за этой кококружности каждая окрестность \ (B \) содержит другой изоморфный пузырьковый кластер \ (B ‘\), в котором одна из двух компонент \ (G {\ setminus} \ {e_1, e_2 \} \) повернута. на некоторый небольшой угол \ (\ varepsilon \) по отношению к другому по кругу, содержащему \ (e_1 \) и \ (e_2 \).\ (B ‘\) имеет ту же общую длину дуги, что и \ (B \), и все его пузыри имеют тот же объем и давление, что и в \ (B \), поэтому он имеет ту же энергию, что и \ (B \). Для любой окрестности \ (B \) будет достаточно малая, но отличная от нуля величина вращения \ (\ varepsilon \), такая, что повернутый кластер принадлежит этой окрестности. Следовательно, \ (B \) не может быть единственной конфигурацией с минимальной энергией в любой окрестности: в лучшем случае она находится в нейтральном равновесии и не может быть стабильной или метастабильной. \(\квадратный \)
Для графов, которые являются 3-связными, мы не знаем, всегда ли наша конструкция создает пузырьковые кластеры, которые являются стабильными или метастабильными, или, альтернативно, образуют ли графы или стабильные или метастабильные пузырьковые кластеры ограниченные подклассы 3-регулярных 3-связных плоских графов. .В неустойчивых равновесиях существуют трехсвязные пузырьковые кластеры [23, 58]; однако известные конструкции для этих кластеров включают длинные тонкие пузыри, которые не содержат окружностей, касающихся каждой стороны пузыря (рис. 18), поэтому эти нестабильные кластеры не могут быть созданы с помощью нашего метода упаковки кругов.
Рис. 18Нестабильный кластер мыльных пузырей, в который многие пузыри не вписаны в круги, что показывает, что он не может быть создан как диаграмма мощности, инвариантная Мёбиуса для упаковки кругов
7 идей для улучшения вашей учебной программы по рисованию
Одна из лучших особенностей курсов AOEU — это то, что учителя рисования со всего мира собираются вместе, чтобы делиться, учиться и улучшать свои практики.Всегда приятно познакомиться с этими творческими, увлеченными учителями, полными удивительных идей!
Один из моих любимых уроков — это «Студия: рисование». Снова и снова я испытываю трепет перед занятиями по искусству и уроками, которые они придумывают для своего класса. Сегодня семь учеников делятся идеями, чтобы вывести навыки рисования ваших учеников и ваш учебный план на новый уровень.
Вот 7 творческих идей, которые родились в Студии AOEU: Курс рисования.
1.Сыграйте в «Drawing Jeopardy».
Эта идея принадлежит Студии рисования Донны Бэнкс. Донна создала потрясающую игру «Рисование опасности», чтобы заинтересовать своих учеников. Она включила вопросы и ответы, основанные на концепциях рисования, техниках, словарном запасе и многом другом.
Вот что Донна сказала о своем учебном пособии.
«Физическое игровое поле слабо имитирует игровой экран из телешоу. Это яркий коллаж, показывающий ряд инструментов для рисования и техник, вдохновляющих на игру.Я использовал смелые цвета для оформления доски и добавил блестящую бахрому, чтобы привлечь студентов. Учетные карточки приклеиваются с помощью точек клея с низким уровнем липкости. Таким образом, ответы и категории можно просто поменять местами, будь то в целях дифференциации или обучения разным предметам ».
Игра предназначена для игры в классе, где учитель выступает в роли ведущего игрового шоу, а ученики разделены на команды. Побеждает команда с наиболее правильными ответами на вопросы. Это такой творческий способ научить студентов терминам, которые они будут использовать во время учебы по рисованию.
2. Поразмышляйте о визуальном опыте ведения дневника.
Студенты в студии: курс рисования делает заметки в визуальном журнале. Происходящее обучение является не чем иным, как зрелищным, поскольку учащиеся систематизируют свои визуальные заметки по-своему. Студентка Даниэла Чироне отлично справилась со своим первым заданием в журнале. Ее размышления о процессе, часть которых можно увидеть ниже, показывают, насколько она выросла.
«Я официально столкнулся со своим страхом рисовать в альбоме для рисования, и мне действительно очень понравился этот процесс! Я писал много заметок во время просмотра видео и чтения.Это начало расслаблять меня и уменьшать беспокойство по поводу мыслей «С чего начать?».
Я проснулся рано в субботу утром, чтобы начать свой визуальный дневник. Он лежал на кухонном столе, пока варил кофе. И снова я подумал: «С чего начать?» Я вспомнил комментарии и отзывы прошлой недели о том, как испачкать бумагу, запачкав ее. Итак, я пролил кофе на первую страницу своего визуального журнала.
Как только я действительно начал работать, продолжать работать стало поразительно легко.Я просто нарисовал следующее, что пришло в голову. На этот раз у меня не было предвзятого плана, я просто создал. Моя первая страница в альбоме для рисования была вдохновлена активизацией всех моих чувств. В воздухе витал аромат свежего кофе. Ко мне разложили кофейные зерна вокруг моего блокнота и стола. Я пробовал кофе, проливал его, читал этикетку на кофейных зернах. Это был момент, когда я жил, и я запечатлел все это на своем рисунке ».
Представьте, как если бы ваши ученики размышляли о том, как они создают свои страницы визуального журнала, могли бы углубить их мышление или заставить их взглянуть на вещи по-новому.
3. Посмотрите в лицо своему страху перед хитрыми приемами.
Для многих учителей рисования анатомия и перспектива не являются любимыми предметами преподавания. Однако студентка Кристин Синтула объединила эти два урока в динамичный урок.
Она поделилась: «Я решила объединить изучение анатомии на прошлой неделе с акцентом на перспективе на этой неделе. Меня всегда вдохновляли рисунки Микеланджело Буонарроти. Итак, я попытался добавить цифры, показывающие отчаяние и отчаяние, падение с лестницы, которой нет конца.”
Чтобы успешно завершить этот рисунок, Кристина сфотографировала две позы, которые, по ее мнению, придадут рисованию силу и эмоции. Она позировала на своей лестнице, чтобы нарисовать перспективу лестницы.
Подумайте, как ваши ученики могли бы сделать свои собственные эталонные фотографии, чтобы помочь в рисовании сложных предметов. Когда у учащихся есть возможность делать снимки, из которых они рисуют, это беспроигрышный вариант!
Если вы хотите освежить свои анатомические навыки, ознакомьтесь с учебным пакетом Drawing the Human Form PRO.Вы узнаете, как научить своих учеников пропорциям, структуре и позированию и избавиться от страха при реалистичном рисовании.
4. Сделайте ремикс рисунка одноклассника.
Студия: Студентка рисования Карен Мелвин была вдохновлена коллажем и рисованием одноклассницы Роби Нордман. Она решила использовать вдохновение, чтобы пойти в своем собственном направлении. Вот кое-что из того, что она сказала об этом процессе.
«Я решил нарисовать свой дом в линейной перспективе.Вдохновленный созданным Роби коллажем, я хотел попробовать использовать коллаж для большей части изображения. Я собрал множество страниц журналов и книг и использовал глянцевый материал, чтобы склеить части коллажа. Заполнить области коллажем нужного размера было непросто. Чтобы решить эту проблему, я использовал кальку, чтобы обвести область, которую хотел заполнить. Затем я зажал кальку и обрывок коллажа вместе и вырезал их. Когда я преподаю со студентами перспективный проект коллажа, я планирую использовать этот трюк.Я также буду поощрять их добавлять свои собственные истории и исследовать различные средства массовой информации, поскольку они добавляют цвет и текстуру в свои работы ».
Представьте, что ученики могут использовать работу друг друга как отправную точку. Поток идей был бы невероятным.
5. Используйте свет, цвет и текстуру.
Студентка Кристи Хиртен проделала потрясающую работу, экспериментируя со светом, цветом и текстурой во время одного из наших уроков. Вот что она говорит об этом опыте.
«Я очень горжусь реалистичностью и внешним видом своего рисунка. Мне очень нравилось рисовать этот рисунок, и он занимал большую часть моей недели. Было включено довольно много деталей. Фотографии, которые я сделал для этого задания, тоже были очень интересными. Я использовал аквариум и цветную полиэтиленовую пленку, чтобы окрасить воду. Мыло и руки создают впечатление, что вещи ускользают из кончиков ваших пальцев. Было сложно уловить количество деталей в пузырьках на этом рисунке.Но опять же, взгляд на это с точки зрения линий, формы и цвета очень помог ».
Мы с другими учениками были взволнованы, увидев, что мышление и рисунок Кристи перешли на новый уровень. Подумайте, как вы можете подтолкнуть своих учеников, потребовав от них работать в рамках этих параметров.
6. Пусть ваши ученики поэкспериментируют со СМИ.
Портретная живопись может напугать студентов. Приятно видеть, как разные люди подходят к решению этой задачи.Одним из моих любимых решений стала работа Студии: студентка рисования Кэтлин Флинн. Кэтлин проделала невероятную работу по объединению анатомии с портретной живописью. Она использовала смешанные материалы для рисования, в том числе перо и чернила, графит и масляную пастель, чтобы создать сильную серию работ в витрине своего учителя. Вот что она пишет об опыте.
«На сегодняшний день и в рамках этого курса я повторно посетил и исследовал несколько средств массовой информации. Я впервые использовал спиртовые маркеры для визуализации формы и обнаружил, что пористая бумага плохо работает с этим носителем.Я использовал цветные чернильные ручки вместо традиционной черной ручки. Вылупление кистей с тонкими кончиками и разбавленными чернилами очень удовлетворительное и оказалось менее утомительным для пальцев и рук. Масляную пастель в мелком масштабе сложно, но растушевывая лепешку, а не пальцем, можно получить приятный эффект ».
Поощрение учеников к экспериментам с различными средствами массовой информации — один из способов помочь им развить свои навыки. Даже если эксперимент не удался, они все равно кое-чему научились!
7.Объединяйте различные техники.
Всегда приятно видеть, когда ученик объединяет свои новые знания и навыки в успешное финальное произведение. Я был взволнован, когда ученик Грег Пайала поделился своим учителем. Он объединил элементы курса в потрясающую заключительную работу, которая вдохновила всех нас.
Грег пишет: «Я использовал несколько техник и средств массовой информации для создания финальной части. Я намеревался продемонстрировать различные материалы и методы, которые мы использовали в течение семестра.Первая панель — графитовая, вторая — маркер, а третья — техническая ручка с акварельной заливкой. Я создал каждую панель отдельно, используя метод сетки. Затем я связал их как одно целое. Я действительно хотел, чтобы каждая панель стояла сама по себе, но при этом работала вместе как единое целое ».
Призовите своих учеников использовать несколько техник в одном упражнении, чтобы вывести их из зоны комфорта.
Одна вещь, которую мы все узнаем на этих онлайн-курсах, заключается в том, что «вместе мы ИСКУСим лучше.«Я говорю это годами, но студентка AOEU, Кэтлин Флинн, прекрасно сказала это, подытоживая свой опыт в курсе:
«Я считаю, что важно поддерживать сеть поддерживающих учителей. Я до сих пор помню коллег, с которыми я делила студийное пространство в аспирантуре. Что-то особенное происходит, когда люди встречаются лицом к лицу в общем пространстве, а не в Интернете. Однако личности в этом классе сделали его менее безличным, чем онлайн-уроки, которые я посещал в прошлом. Люди здесь были действительно честными, благосклонными и исключительно щедрыми в обмене ресурсами.Я всегда буду ценить и восхищаться этой замечательной группой художников и учителей. Спасибо всем!»
Я надеюсь, что эти идеи вызовут у вас новые мысли в следующем учебном году. Я знаю, что работа учителей по всей стране, безусловно, меня вдохновляет!
Как в настоящее время вы обучаете своих учеников технике рисования?
Думали ли вы о студийном курсе AOEU?
Как делать пузыри | 3+ рецепта пузырей и трюки с пузырями
УЗНАТЬ О пузыряхЧто такое пузыри?
Пузырьки — это карманы с мылом и водой, наполненные воздухом.Когда мыло и вода смешиваются вместе и в смесь вдувается воздух, мыло образует тонкую пленку или стенку и задерживает воздух, создавая пузырь.
Мыльные пузыри — не единственный вид пузырей. Вы можете найти пузыри во многих жидкостях. Вы можете увидеть маленькие пузырьки в простой воде, но они всегда будут в воде или плавающими на поверхности воды, а не в воздухе.
В содовой тоже есть пузыри. Особенность мыльных пузырей в том, что они могут свободно парить в воздухе; они не обязательно должны касаться воды или другой жидкости, как большинство пузырьков.Можете ли вы найти другие пузыри вокруг своего дома? А что насчет чего-то круглого и наполненного воздухом, как пузырь?
(Некоторые примеры — шары, воздушные шары и пузырчатая пленка.)
Как мыло превращает воду в пузыри? Мыло снижает поверхностное натяжение воды, чем обычно.
Он также образует очень тонкую пленку, более гибкую, чем вода. Когда воздух попадает под поверхность смеси мыла и воды, гибкая кожа растягивается в форме шара (круглой, как шар), образуя пузырь!
Вы можете увидеть гибкую кожу, которая образует пузырь, окунув пузырчатую палочку в раствор пузырьков.Когда вы его вытащите, отверстие заполнится эластичной пленкой из жидкости. Если вы осторожно подуйте на кожу, вы надуете пузырь!
Что происходит с пузырями?
Поскольку пузыри состоят из мыла и воды, они могут существовать только до тех пор, пока остается вода. В сухом воздухе вода испаряется — она впитывается сухим воздухом вокруг пузыря, и кожа пузыря становится все тоньше и тоньше, пока, наконец, не лопнет!
Пузырьки появляются не только при испарении.Все, что высохнет, может их лопнуть. Когда пузырь плывет по воздуху и приземляется на ваш палец, стебель сухой травы, стену вашего дома или шерсть вашего питомца, пузырь лопается.
Когда что-то острое и сухое касается пузыря, оно протыкает кожу пузыря, весь воздух выходит из него, и пузырек исчезает! Чтобы узнать, как прикоснуться к пузырю, не лопнув его, выполните трюк 2 в эксперименте «Уловки пузыря».
Почему пузыри круглые?
Пузырьки, которые плавают в воздухе и ни к чему не прикреплены, всегда круглые, потому что тонкая стенка мыла втягивается внутрь, а воздух внутри нее выталкивается наружу.Пузырь всегда пытается занять как можно меньше места и удержать как можно больше воздуха.
Сфера, имеющая форму круглого шара в форме пузыря, — лучший способ занять немного места и удержать много воздуха. Даже когда пузырек имеет форму квадрата или другой формы, как в Уловке 1 из эксперимента с пузырями, он всегда превращается в круглую сферу, как только взлетает в воздух. Квадратный пузырь займет больше места, чем круглый.
Иногда пузыри не круглые.Иногда ветер придает им разные формы. Когда пузыри окружены множеством других пузырей, те, что в середине, сжимаются в другие формы, например, квадраты или шестиугольники (формы с шестью сторонами).
Попробуйте надуть много пузырей рядом друг с другом в неглубоком контейнере и посмотрите, есть ли какие-нибудь не круглые. Если вы лопнете пузыри снаружи, пузыри внутри больше не будут раздавлены, и они снова вытолкнутся, превратившись в круглые пузыри!
Рабочий лист пузырьков
Чтобы получить больше удовольствия от надувания пузырей, используйте этот рабочий лист, чтобы найти общие объекты, из которых можно делать пузыри.Дети также могут найти другие предметы, из которых можно делать пузыри, и нарисовать их в отведенном для этого месте.
Страница не найдена | LACMA
«Метрополис II» Криса Бёрдена — это мощная кинетическая скульптура, созданная по образцу фа…
Чревовещание основывается на путанице между зрением и слухом, кукловодом и…
Каулин Смит — междисциплинарная художница из Лос-Анджелеса, чьи работы отражают…
На выставке LACMA впервые за почти 20 лет, медленно меняющееся повествование…
View From Here: Recent Acquisitions представляет подборку из 16 недавно приобретенных работ…
Ёситомо Нара — один из самых любимых японских художников своего поколения.Его…
Работы До Хо Су вызывают физическое проявление памяти, исследуя идеи…
Пожалуй, самый доминирующий вид искусства за последние 100 лет, фильм имеет важное значение…
Утренники вторника
Наслаждайтесь концертами ведущих международных и местных ансамблей в программах…
Искусство и музыка, Джаз в LACMA, Latin Sounds, Sunday Live
Живопись, эстамп, коллаж и многое другое — не выходя из дома!…
Rain Room от Random International (2012) — это захватывающая среда вечного…
Rain Room
«150 портретных тонов» Марка Брэдфорда, композиция размером с фреску, содержащая элементы…
Первый крупный проект искусства Фиджи, который будет смонтирован в Соединенных Штатах…
Работы художника Роберта Ирвина за последние пять десятилетий исследовали восприятие…
В фильме Барбары Крюгер «Без названия» (Shafted) характерно ее особенное использование рекламы…
С февраля 2017 года по январь 2019 года художница из Нью-Йорка Вера Люттер была приглашена…
Band (2006) может квалифицироваться как magnum opus Ричарда Серры, представляя самый полный…
Коллекция современного искусства LACMA, в которой представлены преимущественно европейские и американские произведения искусства…
Группа закупок и члены Художественного совета LACMA разделяют глубокую близость к…
Художественные советы, Группы по приобретению, Искусство Ближнего Востока: СОВРЕМЕННО, Азиатский совет по искусству, Совет по костюмам, Совет по декоративному искусству и дизайну, LENS: Совет фотографии, Совет по современному и современному искусству, Совет по гравюрам и рисункам
Добро пожаловать на страницу вакансий в Художественном музее округа Лос-Анджелес.
